Totes les persones durant la seva vida es troben amb cossos que es troben en un dels tres estats agregats de la matèria. L'estat d'agregació més senzill d'estudiar és el gas. A l'article, considerarem el concepte de gas ideal, donarem l'equació d'estat del sistema i també prestarem una mica d'atenció a la descripció de la temperatura absoluta.
Estat gasós de la matèria
Cada alumne té una bona idea de quin estat de la matèria està parlant quan escolta la paraula "gas". Aquesta paraula s'entén com un cos capaç d'ocupar qualsevol volum que se li proporcioni. No és capaç de mantenir la seva forma, perquè no pot resistir ni la més mínima influència externa. A més, el gas no reté volum, cosa que el distingeix no només dels sòlids, sinó també dels líquids.
Com un líquid, un gas és una substància fluida. En el procés de moviment dels cossos sòlids en gasos, aquests últims impedeixen aquest moviment. La força resultant s'anomena resistència. El seu valor depènvelocitat del cos en el gas.
Exemples forts de gasos són l'aire, el gas natural utilitzat per escalfar llars i cuinar, els gasos inerts (Ne, Ar) que s'utilitzen per omplir tubs lluminosos publicitaris o que s'utilitzen per crear un entorn inert (no agressiu, protector) durant la soldadura..
Gasolina ideal
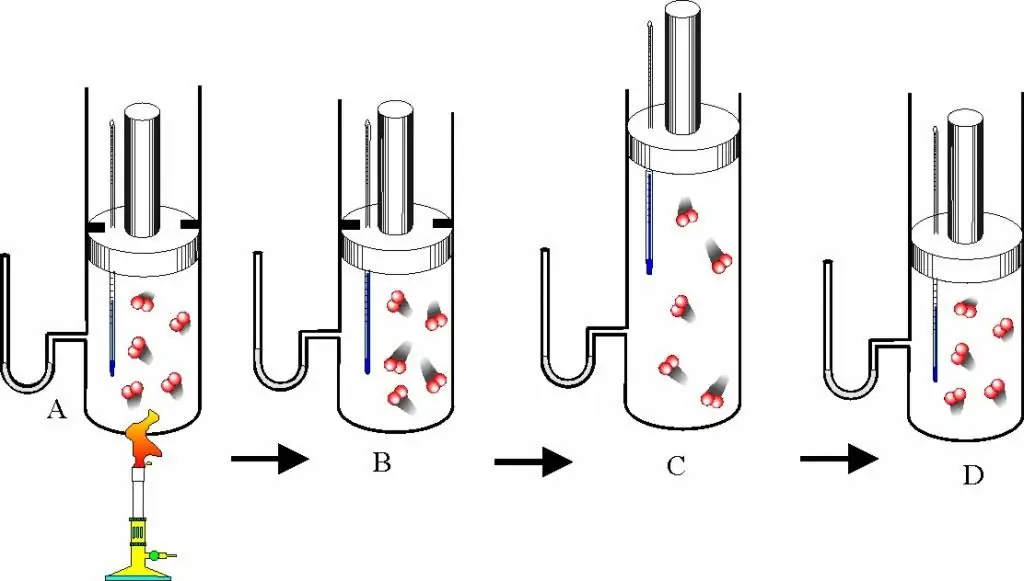
Abans de procedir a la descripció de les lleis dels gasos i de l'equació d'estat, hauríeu d'entendre bé la qüestió de què és un gas ideal. Aquest concepte s'introdueix a la teoria cinètica molecular (MKT). Un gas ideal és qualsevol gas que compleixi les característiques següents:
- Les partícules que la formen no interaccionen entre elles excepte en les col·lisions mecàniques directes.
- Com a conseqüència del xoc de partícules amb les parets del vaixell o entre elles, es conserven l'energia cinètica i el moment, és a dir, la col·lisió es considera absolutament elàstica.
- Les partícules no tenen dimensions, però tenen una massa finita, és a dir, són semblants als punts materials.
És natural que qualsevol gas no sigui ideal, sinó real. No obstant això, per resoldre molts problemes pràctics, aquestes aproximacions són força vàlides i es poden utilitzar. Hi ha una regla empírica general que diu: independentment de la naturalesa química, si un gas té una temperatura superior a la temperatura ambient i una pressió de l'ordre de l'atmosfèrica o inferior, llavors es pot considerar ideal amb gran precisió i es pot utilitzar per descriure això.fórmula de l'equació d'estat dels gasos ideals.
Llei Clapeyron-Mendeleev
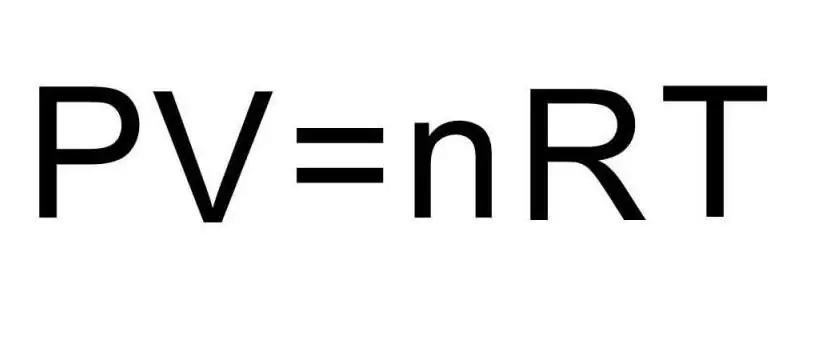
Les transicions entre diferents estats agregats de la matèria i processos dins d'un sol estat agregat es gestionen mitjançant la termodinàmica. La pressió, la temperatura i el volum són tres magnituds que defineixen de manera única qualsevol estat d'un sistema termodinàmic. La fórmula de l'equació d'estat d'un gas ideal combina aquestes tres quantitats en una única igu altat. Escrivim aquesta fórmula:
PV=nRT
Aquí P, V, T - pressió, volum, temperatura, respectivament. El valor de n és la quantitat de substància en mols, i el símbol R indica la constant universal dels gasos. Aquesta igu altat mostra que com més gran sigui el producte de la pressió i el volum, més gran ha de ser el producte de la quantitat de substància i la temperatura.

La fórmula per a l'equació d'estat d'un gas s'anomena llei de Clapeyron-Mendeleiev. El 1834, el científic francès Emile Clapeyron, resumint els resultats experimentals dels seus predecessors, va arribar a aquesta equació. No obstant això, Clapeyron va utilitzar una sèrie de constants, que Mendeleiev va substituir més tard per una: la constant de gas universal R (8, 314 J / (molK)). Per tant, a la física moderna, aquesta equació rep el nom dels noms de científics francesos i russos.

Altres formes d'equació
A d alt, hem escrit l'equació d'estat de Mendeleiev-Clapeyron per a un gas ideal en la forma generalment acceptada iforma convenient. Tanmateix, en problemes de termodinàmica, sovint es pot requerir una forma lleugerament diferent. A continuació s'escriuen tres fórmules més, que segueixen directament de l'equació escrita:
PV=NkBT;
PV=m/MRT;
P=ρRT/M.
Aquestes tres equacions també són universals per a un gas ideal, només en elles apareixen quantitats com la massa m, la massa molar M, la densitat ρ i el nombre de partícules N que formen el sistema. El símbol kB aquí denota la constant de Boltzmann (1, 3810-23J/K).
Llei de Boyle-Mariotte
Quan Clapeyron va elaborar la seva equació, es va basar en les lleis dels gasos que s'havien descobert experimentalment diverses dècades abans. Una d'elles és la llei Boyle-Mariotte. Reflecteix un procés isotèrmic en un sistema tancat, com a resultat del qual canvien paràmetres macroscòpics com la pressió i el volum. Si posem T i n constants a l'equació d'estat d'un gas ideal, aleshores la llei dels gasos tindrà la forma:
P1V1=P2V 2
Aquesta és la llei de Boyle-Mariotte, que diu que el producte de pressió i volum es conserva durant un procés isotèrmic arbitrari. En aquest cas, els mateixos valors P i V canvien.
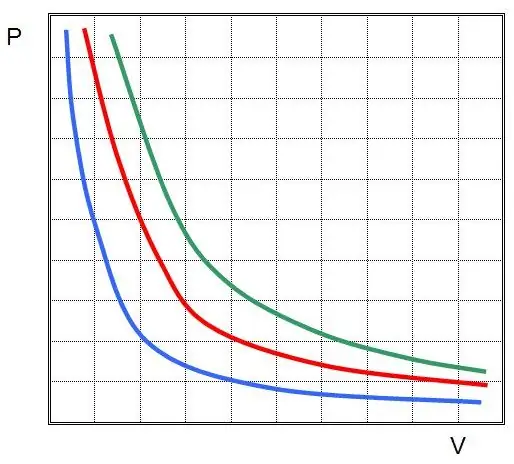
Si traceu P(V) o V(P), les isotermes seran hipèrboles.
Les lleis de Charles i Gay-Lussac
Aquestes lleis descriuen matemàticament isobàric i isòcòricprocessos, és a dir, aquestes transicions entre els estats del sistema de gas, en què es conserven la pressió i el volum, respectivament. La llei de Charles es pot escriure matemàticament de la següent manera:
V/T=const quan n, P=const.
La llei de Gay-Lussac s'escriu de la següent manera:
P/T=const quan n, V=const.
Si les dues igu altats es presenten en forma de gràfic, obtindrem rectes inclinades en algun angle respecte a l'eix x. Aquest tipus de gràfic indica una proporcionalitat directa entre el volum i la temperatura a pressió constant i entre la pressió i la temperatura a volum constant.
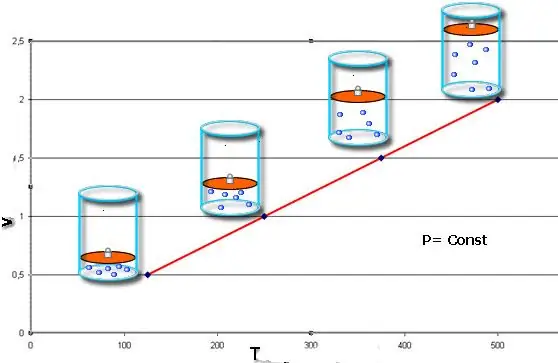
Tingueu en compte que les tres lleis dels gasos considerades no tenen en compte la composició química del gas, així com el canvi en la seva quantitat de matèria.
Temperatura absoluta
A la vida quotidiana, estem acostumats a utilitzar l'escala de temperatura Celsius, ja que és convenient per descriure els processos que ens envolten. Per tant, l'aigua bull a 100 oC i es congela a 0 oC. En física, aquesta escala resulta inconvenient, per tant, s'utilitza l'anomenada escala de temperatura absoluta, que va ser introduïda per Lord Kelvin a mitjans del segle XIX. D'acord amb aquesta escala, la temperatura es mesura en Kelvin (K).
Es creu que a una temperatura de -273, 15 oC no hi ha vibracions tèrmiques d'àtoms i molècules, el seu moviment cap endavant s'atura completament. Aquesta temperatura en graus Celsius correspon al zero absolut en Kelvin (0 K). A partir d'aquesta definiciósegueix el significat físic de la temperatura absoluta: és una mesura de l'energia cinètica de les partícules que formen la matèria, per exemple, àtoms o molècules.
A més del significat físic anterior de la temperatura absoluta, hi ha altres enfocaments per entendre aquesta quantitat. Un d'ells és l'esmentada llei dels gasos de Charles. Escrivim-ho de la forma següent:
V1/T1=V2/T 2=>
V1/V2=T1/T 2.
L'última igu altat diu que a una certa quantitat de substància del sistema (per exemple, 1 mol) i una determinada pressió (per exemple, 1 Pa), el volum del gas determina de manera única la temperatura absoluta. En altres paraules, un augment del volum de gas en aquestes condicions només és possible a causa d'un augment de la temperatura, i una disminució del volum indica una disminució del valor de T.
Recordeu que, a diferència de la temperatura Celsius, la temperatura absoluta no pot ser negativa.
Principi d'Avogadro i mescles de gasos
A més de les lleis dels gasos anteriors, l'equació d'estat d'un gas ideal també condueix al principi descobert per Amedeo Avogadro a principis del segle XIX, que porta el seu cognom. Aquest principi estableix que el volum de qualsevol gas a pressió i temperatura constants ve determinat per la quantitat de substància del sistema. La fórmula corresponent té aquest aspecte:
n/V=const quan P, T=const.
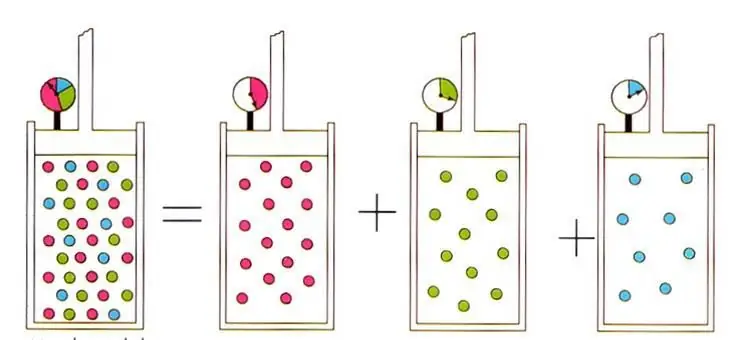
L'expressió escrita condueix a la coneguda llei de D alton de la física de gasos ideals per a les mescles de gasos. Aixòla llei estableix que la pressió parcial d'un gas en una mescla està determinada exclusivament per la seva fracció atòmica.
Exemple de resolució de problemes
En un recipient tancat amb parets rígides que contenia un gas ideal, com a conseqüència de l'escalfament, la pressió augmentava 3 vegades. Cal determinar la temperatura final del sistema si el seu valor inicial era de 25 oC.
Primer, convertim la temperatura de graus Celsius a Kelvin, tenim:
T=25 + 273, 15=298, 15 K.
Com que les parets del recipient són rígides, el procés d'escalfament es pot considerar isocòric. En aquest cas, apliquem la llei Gay-Lussac, tenim:
P1/T1=P2/T 2=>
T2=P2/P1T 1.
Així, la temperatura final es determina a partir del producte de la relació de pressió i la temperatura inicial. Substituint les dades per igu altat, obtenim la resposta: T2=894,45 K. Aquesta temperatura correspon a 621,3 oC.






