El mòdul d'elasticitat és una magnitud física que caracteritza el comportament elàstic d'un material quan se li aplica una força externa en una direcció determinada. El comportament elàstic d'un material significa la seva deformació a la regió elàstica.
Història de l'estudi de l'elasticitat dels materials

La teoria física dels cossos elàstics i el seu comportament sota l'acció de forces externes va ser considerada amb detall i estudiada pel científic anglès del segle XIX, Thomas Young. Tanmateix, el mateix concepte d'elasticitat va ser desenvolupat l'any 1727 pel matemàtic, físic i filòsof suís Leonhard Euler, i els primers experiments relacionats amb el mòdul d'elasticitat es van dur a terme el 1782, és a dir, 25 anys abans del treball de Thomas Jung., del matemàtic i filòsof venecià Jacopo Ricatti.
El mèrit de Thomas Young rau en el fet que va donar a la teoria de l'elasticitat un aspecte modern esvelt, que es va formalitzar posteriorment en forma d'una llei de Hooke simple i després generalitzada.
Característica física de l'elasticitat
Qualsevol cos està format per àtoms, entre els quals actuen les forces d'atracció i repulsió. L'equilibri d'aquestes forces ésl'estat i els paràmetres de la matèria en condicions determinades. Els àtoms d'un cos sòlid, quan se'ls apliquen forces externes de tensió o compressió insignificants, comencen a desplaçar-se, creant una força oposada en direcció i igual en magnitud, que tendeix a tornar els àtoms al seu estat inicial.
En el procés d'aquest desplaçament d'àtoms, l'energia de tot el sistema augmenta. Els experiments mostren que en deformacions petites l'energia és proporcional al quadrat d'aquestes soques. Això vol dir que la força, en ser una derivada respecte a l'energia, resulta ser proporcional a la primera potència de la deformació, és a dir, en depèn linealment. Responent a la pregunta, quin és el mòdul d'elasticitat, podem dir que aquest és el coeficient de proporcionalitat entre la força que actua sobre l'àtom i la deformació que aquesta força provoca. La dimensió del mòdul de Young és la mateixa que la dimensió de pressió (Pascal).
Límit elàstic
Segons la definició, el mòdul d'elasticitat indica quanta tensió cal aplicar a un sòlid perquè la seva deformació sigui del 100%. Tanmateix, tots els sòlids tenen un límit elàstic igual a l'1% de tensió. Això significa que si s'aplica una força adequada i el cos es deforma en una quantitat inferior a l'1%, després de la finalització d'aquesta força, el cos restaura exactament la seva forma i dimensions originals. Si s'aplica massa força, a la qual el valor de deformació supera l'1%, després de la finalització de la força externa, el cos ja no restaurarà les seves dimensions originals. En aquest darrer cas, es parla de l'existència d'una deformació residual, que ésprova que s'ha superat el límit elàstic del material.
Mòdul de Young en acció
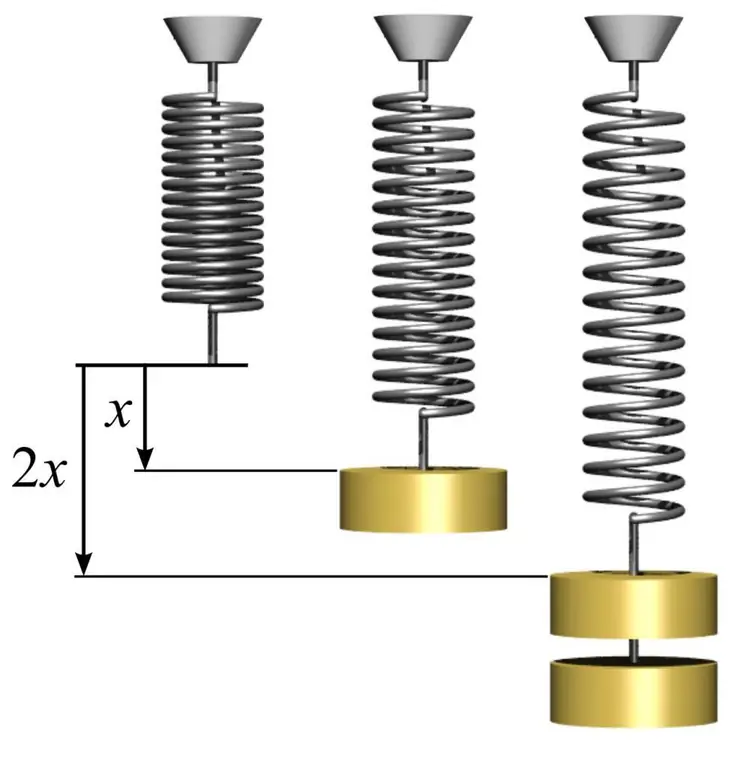
Per determinar el mòdul d'elasticitat, així com per entendre com utilitzar-lo, podeu posar un exemple senzill amb una molla. Per fer-ho, cal agafar una molla metàl·lica i mesurar l'àrea del cercle que formen les seves bobines. Això es fa utilitzant la fórmula senzilla S=πr², on n és pi igual a 3,14 i r és el radi de la bobina de la molla.
A continuació, mesura la longitud de la molla l0 sense càrrega. Si pengeu qualsevol càrrega de massa m1 a una molla, augmentarà la seva longitud fins a un determinat valor l1. El mòdul d'elasticitat E es pot calcular a partir del coneixement de la llei de Hooke mitjançant la fórmula: E=m1gl0/(S(l 1-l0)), on g és l'acceleració de caiguda lliure. En aquest cas, observem que la quantitat de deformació de la molla a la regió elàstica pot superar molt l'1%.
Conèixer el mòdul de Young us permet predir la quantitat de deformació sota l'acció d'un esforç particular. En aquest cas, si pengem una altra massa m2 a la molla, obtenim el següent valor de deformació relativa: d=m2g/ (SE), on d - deformació relativa a la regió elàstica.
Isotropia i anisotropia
El mòdul d'elasticitat és una característica d'un material que descriu la força de l'enllaç entre els seus àtoms i molècules, però un material determinat pot tenir diversos mòduls de Young diferents.
El fet és que les propietats de cada sòlid depenen de la seva estructura interna. Si les propietats són les mateixes en totes les direccions espacials, estem parlant d'un material isòtrop. Aquestes substàncies tenen una estructura homogènia, de manera que l'acció d'una força externa en diferents direccions sobre elles provoca la mateixa reacció del material. Tots els materials amorfs són isòtrops, com ara el cautxú o el vidre.
L'anisotropia és un fenomen que es caracteritza per la dependència de les propietats físiques d'un sòlid o líquid de la direcció. Tots els metalls i aliatges basats en ells tenen una o altra xarxa cristal·lina, és a dir, una disposició ordenada, més que no pas caòtica, dels nuclis iònics. Per a aquests materials, el mòdul d'elasticitat varia en funció de l'eix d'acció de la tensió externa. Per exemple, els metalls amb simetria cúbica, com l'alumini, el coure, la plata, els metalls refractaris i altres, tenen tres mòduls de Young diferents.
Mòdul de cisalla
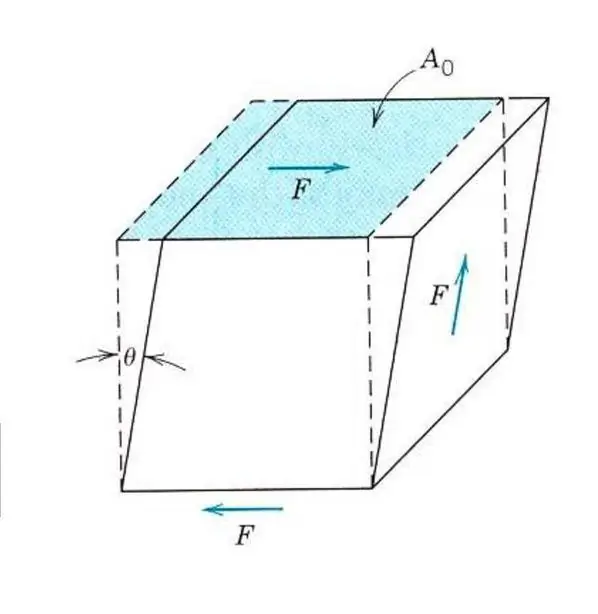
La descripció de les propietats elàstiques fins i tot d'un material isòtrop no requereix el coneixement d'un mòdul de Young. Perquè, a més de la tensió i la compressió, el material es pot veure afectat per esforços de tall o torsions. En aquest cas, reaccionarà de manera diferent a la força externa. Per descriure la deformació per cisalla elàstica, s'introdueix un anàleg del mòdul de Young, mòdul de cisalla o mòdul d'elasticitat del segon tipus.
Tots els materials resisteixen les tensions de cisalla menys que la tensió o la compressió, de manera que el valor del mòdul de cisalla per a ells és 2-3 vegades menor que el valor del mòdul de Young. Així, per al titani, el mòdul de Young del qual és igual a 107 GPa, el mòdul de cisalla ésnomés 40 GPa, per a l'acer aquestes xifres són 210 GPa i 80 GPa, respectivament.
Mòdul d'elasticitat de la fusta

La fusta és un material anisòtrop perquè les fibres de fusta s'orienten en una direcció específica. És al llarg de les fibres on es mesura el mòdul d'elasticitat de la fusta, ja que és 1-2 ordres de magnitud més petit a través de les fibres. El coneixement del mòdul de Young per a la fusta és important i es té en compte a l'hora de dissenyar estructures de panells de fusta.
Els valors del mòdul d'elasticitat de la fusta per a alguns tipus d'arbres es mostren a la taula següent.
| Vista en arbre | Mòdul de Young en GPa |
| Arbre de llorer | 14 |
| Eucaliptus | 18 |
| Cedre | 8 |
| Avet | 11 |
| Pí | 10 |
| Roure | 12 |
Cal tenir en compte que els valors donats poden diferir fins a 1 GPa per a un arbre en concret, ja que el seu mòdul de Young es veu afectat per la densitat de la fusta i les condicions de creixement.

Els mòduls de cisalla per a diverses espècies d'arbres estan en el rang d'1-2 GPa, per exemple, per al pi és d'1,21 GPa, i per al roure 1,38 GPa, és a dir, la fusta pràcticament no resisteix les tensions de cisalla. Aquest fet s'ha de tenir en compte en la fabricació d'estructures portants de fusta, que estan dissenyades per treballar només en tensió o compressió.
Característiques elàstiques dels metalls
En comparació amb el mòdul de Young de la fusta, els valors mitjans d'aquest valor per als metalls i els aliatges són un ordre de magnitud superiors, tal com es mostra a la taula següent.
| Metal | Mòdul de Young en GPa |
| Bronze | 120 |
| Core | 110 |
| Acer | 210 |
| Titani | 107 |
| níquel | 204 |
Les propietats elàstiques dels metalls que tenen una singonia cúbica es descriuen mitjançant tres constants elàstiques. Aquests metalls inclouen coure, níquel, alumini, ferro. Si un metall té una singonia hexagonal, ja es necessiten sis constants per descriure les seves característiques elàstiques.
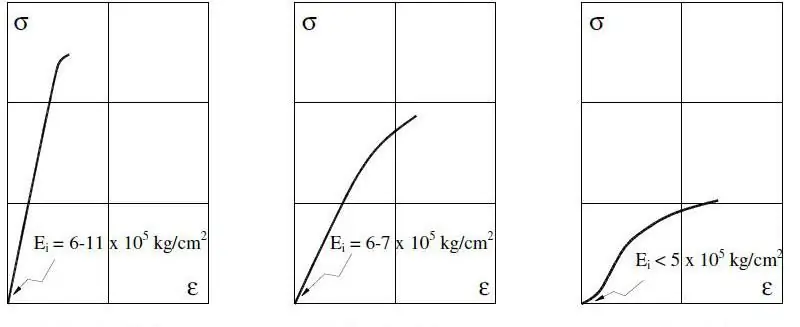
Per als sistemes metàl·lics, el mòdul de Young es mesura amb una tensió del 0,2%, ja que ja es poden produir grans valors a la regió inelàstica.






