La resolució és la capacitat d'un sistema d'imatge per reproduir els detalls d'un objecte i depèn de factors com el tipus d'il·luminació utilitzat, la mida de píxel del sensor i les capacitats de l'òptica. Com més petit sigui el detall del subjecte, més gran serà la resolució necessària de l'objectiu.
Introducció al procés de resolució
La qualitat de la imatge de la càmera depèn del sensor. En poques paraules, un sensor d'imatge digital és un xip dins del cos d'una càmera que conté milions de punts sensibles a la llum. La mida del sensor d'una càmera determina quanta llum es pot utilitzar per crear una imatge. Com més gran sigui el sensor, millor serà la qualitat de la imatge a mesura que es reculli més informació. Normalment, les càmeres digitals s'anuncien al mercat amb mides de sensor de 16 mm, Super 35 mm i de vegades fins a 65 mm.
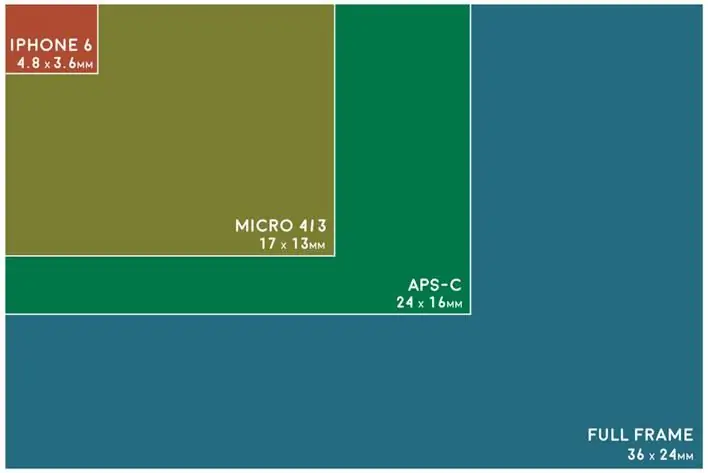
A mesura que augmenta la mida del sensor, la profunditat de camp disminuirà a una obertura determinada, ja que una contrapart més gran requereix que us apropeu aobjecte o utilitzeu una distància focal més llarga per omplir el marc. Per mantenir la mateixa profunditat de camp, el fotògraf ha d'utilitzar obertures més petites.
Aquesta poca profunditat de camp pot ser desitjable, especialment per aconseguir el desenfocament del fons per als retrats, però la fotografia de paisatge requereix més profunditat, cosa que és més fàcil de capturar amb la mida flexible de l'obertura de les càmeres compactes.
Dividir el nombre de píxels horitzontals o verticals d'un sensor indicarà quant espai ocupa cadascun en un objecte i es pot utilitzar per avaluar el poder de resolució de la lent i resoldre les preocupacions dels clients sobre la mida de píxel de la imatge digital del dispositiu. Com a punt de partida, és important entendre què pot limitar realment la resolució del sistema.
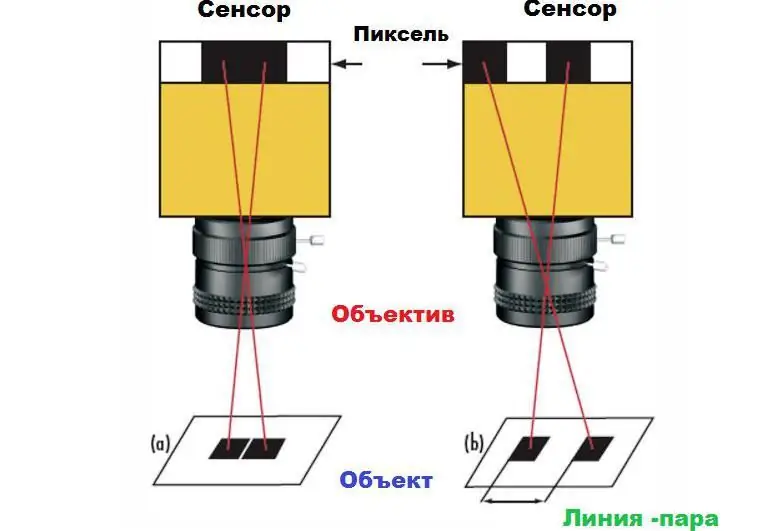
Aquesta afirmació es pot demostrar amb l'exemple d'un parell de quadrats sobre un fons blanc. Si els quadrats del sensor de la càmera s'assignen a píxels veïns, apareixeran com un rectangle gran a la imatge (1a) en lloc de dos quadrats separats (1b). Per distingir els quadrats, cal un espai determinat entre ells, almenys un píxel. Aquesta distància mínima és la màxima resolució del sistema. El límit absolut ve determinat per la mida dels píxels del sensor, així com pel seu nombre.
Característiques de la lent de mesura
La relació entre quadrats blancs i negres alternats es descriu com una parella lineal. Normalment, la resolució ve determinada per la freqüència,mesurat en parells de línies per mil·límetre - lp/mm. Malauradament, la resolució de la lent en cm no és un nombre absolut. Amb una resolució determinada, la capacitat de veure els dos quadrats com a objectes separats dependrà del nivell d'escala de grisos. Com més gran sigui la separació d'escala de grisos entre ells i l'espai, més estable és la capacitat de resoldre aquests quadrats. Aquesta divisió de l'escala de grisos es coneix com a contrast de freqüència.
La freqüència espacial es dóna en lp/mm. Per aquest motiu, calcular la resolució en termes de lp/mm és extremadament útil a l'hora de comparar lents i determinar la millor opció per a determinats sensors i aplicacions. El primer és on comença el càlcul de la resolució del sistema. Començant pel sensor, és més fàcil determinar quines especificacions de lents es necessiten per complir els requisits del dispositiu o d' altres aplicacions. La freqüència més alta que permet el sensor, Nyquist, és efectivament dos píxels o un parell de línies.
La resolució de la lent de definició, també anomenada resolució de l'espai d'imatge del sistema, es pot determinar multiplicant la mida en Μm per 2 per crear un parell i dividint per 1000 per convertir a mm:
lp/mm=1000/ (2 x píxels)
Els sensors amb píxels més grans tindran límits de resolució més baixos. Els sensors amb píxels més petits funcionaran millor segons la fórmula de resolució de la lent anterior.
Àrea del sensor actiu
Podeu calcular la resolució màxima de l'objectevisualització. Per fer-ho, cal distingir entre indicadors com ara la relació entre la mida del sensor, el camp de visió i el nombre de píxels del sensor. La mida d'aquest últim fa referència als paràmetres de l'àrea activa del sensor de la càmera, normalment determinats per la mida del seu format.
No obstant això, les proporcions exactes variaran segons la relació d'aspecte i les mides nominals dels sensors només s'han d'utilitzar com a orientació, especialment per a lents telecèntriques i grans augments. La mida del sensor es pot calcular directament a partir de la mida dels píxels i el nombre actiu de píxels per dur a terme una prova de resolució de la lent.
La taula mostra el límit de Nyquist associat a les mides de píxels que es troben en alguns sensors d'ús molt habitual.
| Mida de píxels (µm) | Límit de Nyquist acoblat (lp/mm) |
| 1, 67 | 299, 4 |
| 2, 2 | 227, 3 |
| 3, 45 | 144, 9 |
| 4, 54 | 110, 1 |
| 5, 5 | 90, 9 |
A mesura que la mida dels píxels disminueix, el límit de Nyquist associat en lp/mm augmenta proporcionalment. Per determinar el punt resoluble mínim absolut que es pot veure en un objecte, s'ha de calcular la relació entre el camp de visió i la mida del sensor. Això també es coneix com a augment primari.sistemes (PMAG).
La relació associada amb el sistema PMAG permet escalar la resolució de l'espai de la imatge. Normalment, quan es dissenya una aplicació, no s'especifica en lp/mm, sinó en micres (µm) o fraccions de polzada. Podeu s altar ràpidament a la resolució final d'un objecte utilitzant la fórmula anterior per facilitar l'elecció de la resolució de la lent z. També és important tenir en compte que hi ha molts factors addicionals i que la limitació anterior és molt menys propensa a errors que la complexitat de tenir en compte molts factors i calcular-los mitjançant equacions.
Calculeu la distància focal
La resolució d'una imatge és el nombre de píxels que hi ha. Designat en dues dimensions, per exemple, 640X480. Els càlculs es poden fer per separat per a cada dimensió, però per simplificar-ho sovint es redueix a un. Per fer mesures precises en una imatge, heu d'utilitzar un mínim de dos píxels per a cada àrea més petita que vulgueu detectar. La mida del sensor es refereix a un indicador físic i, per regla general, no s'indica a les dades del passaport. La millor manera de determinar la mida d'un sensor és mirar els paràmetres de píxels d'aquest i multiplicar-lo per la relació d'aspecte, en aquest cas el poder de resolució de la lent resol els problemes d'una mala presa.
Per exemple, la càmera Basler acA1300-30um té una mida de píxels de 3,75 x 3,75um i una resolució de 1296 x 966 píxels. La mida del sensor és de 3,75 µm x 1296 per 3,75 µm x 966=4,86 x 3,62 mm.
El format del sensor fa referència a la mida física i no depèn de la mida dels píxels. Aquesta configuració s'utilitza perdeterminar amb quina lent és compatible la càmera. Perquè coincideixin, el format de la lent ha de ser superior o igual a la mida del sensor. Si s'utilitza una lent amb una relació d'aspecte més petita, la imatge experimentarà vinyeta. Això fa que les zones del sensor fora de la vora del format de la lent es tornin fosques.
Selecció de píxels i càmera

Per veure els objectes de la imatge, hi ha d'haver prou espai entre ells perquè no es fusionin amb els píxels veïns, en cas contrari no es poden distingir entre ells. Si els objectes són d'un píxel cadascun, la separació entre ells també ha de ser almenys d'un element, és gràcies a això que es forma un parell de línies, que en realitat té dos píxels de mida. Aquesta és una de les raons per les quals és incorrecte mesurar la resolució de càmeres i lents en megapíxels.
En realitat, és més fàcil descriure les capacitats de resolució d'un sistema en termes de freqüència de parell de línies. D'aquesta manera, a mesura que disminueix la mida del píxel, la resolució augmenta perquè podeu posar objectes més petits en elements digitals més petits, tenir menys espai entre ells i, tot i així, resoldre la distància entre els subjectes que feu.
Aquest és un model simplificat de com el sensor de la càmera detecta objectes sense tenir en compte el soroll o altres paràmetres, i és la situació ideal.
Gràfics de contrast MTF
La majoria de les lents no són sistemes òptics perfectes. La llum que travessa una lent pateix un cert grau de degradació. La qüestió és com avaluar-hodegradació? Abans de respondre a aquesta pregunta, cal definir el concepte de "modulació". Aquesta última és una mesura de la lent de contrast a una freqüència determinada. Es podria intentar analitzar imatges del món real preses a través d'una lent per determinar la modulació o el contrast de detalls de diferents mides o freqüències (espaiat), però això és molt poc pràctic.
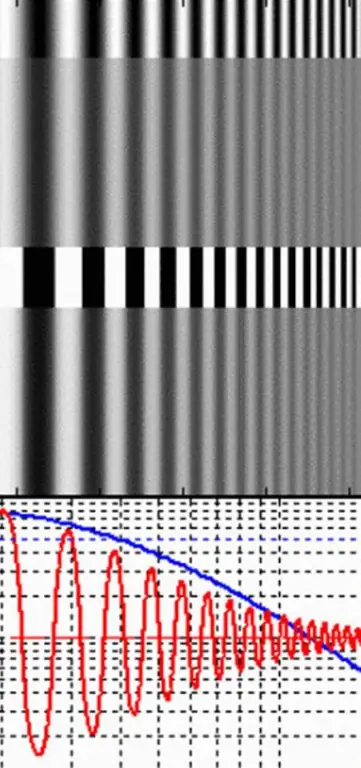
En canvi, és molt més fàcil mesurar la modulació o el contrast per a parells de línies blanques i fosques alternes. S'anomenen gelosia rectangular. L'interval de línies en una xarxa d'ona rectangular és la freqüència (v), per a la qual la funció de modulació o contrast de la lent i la resolució es mesuren en cm.
La quantitat màxima de llum vindrà de les bandes clares i la mínima de les bandes fosques. Si la llum es mesura en termes de brillantor (L), la modulació es pot determinar segons l'equació següent:
modulació=(Lmax - Lmin) / (Lmax + Lmin), on: Lmax és la brillantor màxima de les línies blanques a la reixa i Lmin és la brillantor mínima de les fosques.
Quan la modulació es defineix en termes de llum, sovint s'anomena contrast de Michelson perquè pren la relació de luminància de les bandes clares i fosques per mesurar el contrast.
Per exemple, hi ha una reixa d'ona quadrada d'una determinada freqüència (v) i modulació, i un contrast inherent entre les zones fosques i clares reflectides per aquesta reixa a través de la lent. La modulació de la imatge i, per tant, el contrast de la lent es mesura per a una freqüència determinadabarres (v).
La funció de transferència de modulació (MTF) es defineix com la modulació M i de la imatge dividida per la modulació de l'estímul (objecte) M o, tal com es mostra a l'equació següent.
|
MTF (v)=M i / M 0 |
USF s'imprimeixen en paper làser brillant al 98%. El tòner d'impressora làser negre té una reflectància d'un 10%. Per tant, el valor de M 0 és del 88%. Però com que la pel·lícula té un rang dinàmic més limitat en comparació amb l'ull humà, és segur suposar que M 0 és essencialment el 100% o 1. Per tant, la fórmula anterior es resumeix en el següent més equació simple:
|
MTF (v)=Mi |
Per tant, la lent MTF per a una freqüència de reixeta determinada (v) és simplement la modulació de reixeta mesurada (Mi) quan es fotografia a través d'una lent a la pel·lícula.
Resolució del microscopi
La resolució d'un objectiu de microscopi és la distància més curta entre dos punts diferents del camp de visió de l'ocular que encara es poden distingir com a objectes diferents.
Si dos punts estan més a prop que la vostra resolució, apareixeran difusos i les seves posicions seran inexactes. El microscopi pot oferir un gran augment, però si les lents són de mala qualitat, la mala resolució resultant degradarà la qualitat de la imatge.
A continuació hi ha l'equació d'Abbe, on la resolucióLa potència de la lent z d'un microscopi és la potència de resolució igual a la longitud d'ona de la llum utilitzada dividida per 2 (l'obertura numèrica de l'objectiu).
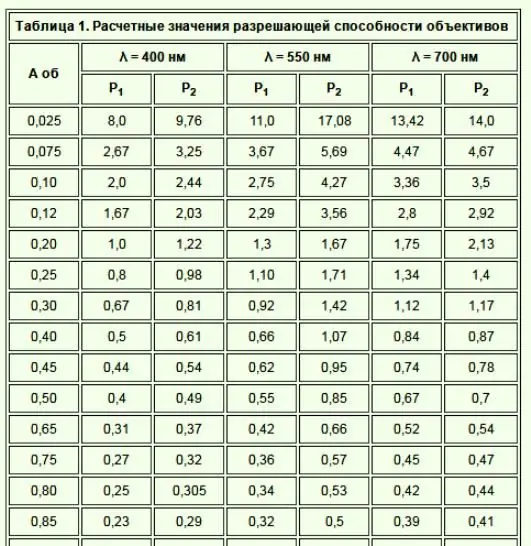
Diversos elements afecten la resolució d'un microscopi. Un microscopi òptic configurat amb un augment elevat pot produir una imatge borrosa, però encara té la màxima resolució de la lent.
L'obertura digital d'una lent afecta la resolució. El poder de resolució d'un objectiu de microscopi és un nombre que indica la capacitat d'una lent per recollir llum i resoldre un punt a una distància fixa de l'objectiu. El punt més petit que es pot resoldre amb la lent és proporcional a la longitud d'ona de la llum recollida dividida pel nombre d'obertura numèrica. Per tant, un nombre més gran correspon a una major capacitat de la lent per detectar un punt excel·lent en el camp de visió. L'obertura numèrica de la lent també depèn de la quantitat de correcció de l'aberració òptica.
Resolució de la lent del telescopi
Com un embut de llum, un telescopi és capaç de recollir la llum en proporció a l'àrea del forat, aquesta propietat és la lent principal.
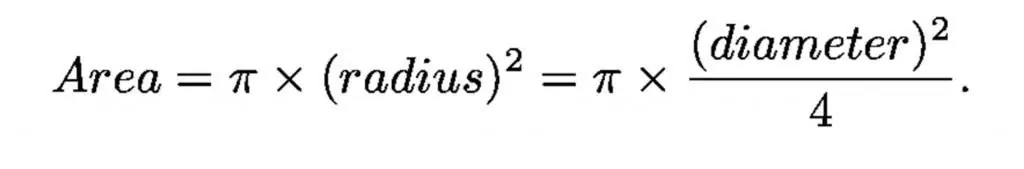
El diàmetre de la pupil·la adaptada a la foscor de l'ull humà és d'una mica menys d'1 centímetre i el diàmetre del telescopi òptic més gran és de 1.000 centímetres (10 metres), de manera que el telescopi més gran té una col·lecció un milió de vegades més gran àrea que l'ull humà.

És per això que els telescopis veuen objectes més febles que els humans. I tingueu dispositius que acumulin llum mitjançant sensors de detecció electrònica durant moltes hores.
Hi ha dos tipus principals de telescopis: refractors basats en lents i reflectors basats en mirall. Els telescopis grans són reflectors perquè els miralls no han de ser transparents. Els miralls telescopis es troben entre els dissenys més precisos. L'error permès a la superfície és d'aproximadament 1/1000 de l'amplada d'un cabell humà, a través d'un forat de 10 metres.
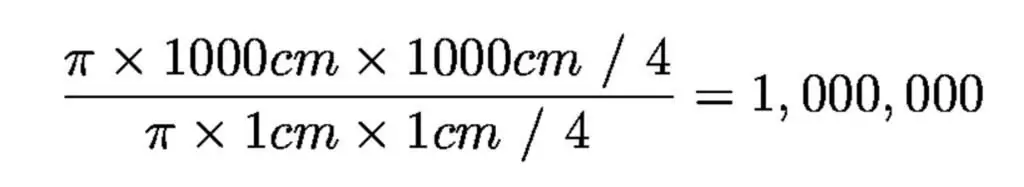
Els miralls solien estar fets amb grans lloses de vidre gruixudes per evitar que s'enfonsin. Els miralls actuals són prims i flexibles, però estan controlats per ordinador o d'una altra manera segmentats i alineats per un control informàtic. A més de la tasca de trobar objectes febles, l'objectiu de l'astrònom també és veure'n els detalls. El grau en què es poden reconèixer els detalls s'anomena resolució:
- Imatges borroses=mala resolució.
- Imatges clares=bona resolució.
A causa de la naturalesa ondulatòria de la llum i dels fenòmens anomenats difracció, el diàmetre del mirall o de la lent d'un telescopi limita la seva resolució final en relació amb el diàmetre del telescopi. La resolució aquí significa el detall angular més petit que es pot reconèixer. Els valors petits corresponen a un excel·lent detall de la imatge.
Els radiotelescopis han de ser molt grans per oferir una bona resolució. L'atmosfera terrestre ésimatges turbulentes i desdibuixades del telescopi. Els astrònoms terrestres poques vegades poden assolir la màxima resolució de l'aparell. L'efecte turbulent de l'atmosfera sobre una estrella s'anomena visió. Aquesta turbulència fa que les estrelles "brillin". Per evitar aquests desenfocaments atmosfèrics, els astrònoms llancen telescopis a l'espai o els col·loquen a altes muntanyes amb condicions atmosfèriques estables.
Exemples de càlcul de paràmetres
Dades per determinar la resolució de l'objectiu de Canon:
- Mida dels píxels=3,45 µm x 3,45 µm.
- píxels (H x V)=2448 x 2050.
- Camp de visió desitjat (horitzontal)=100 mm.
- Límit de resolució del sensor: 1000/2x3, 45=145 lp/mm.
- Dimensions del sensor: 3,45x2448/1000=8,45 mm3, 45x2050/1000=7,07 mm.
- PMAG:8, 45/100=0,0845 mm.
- Resolució de la lent de mesura: 145 x 0,0845=12,25 lp/mm.
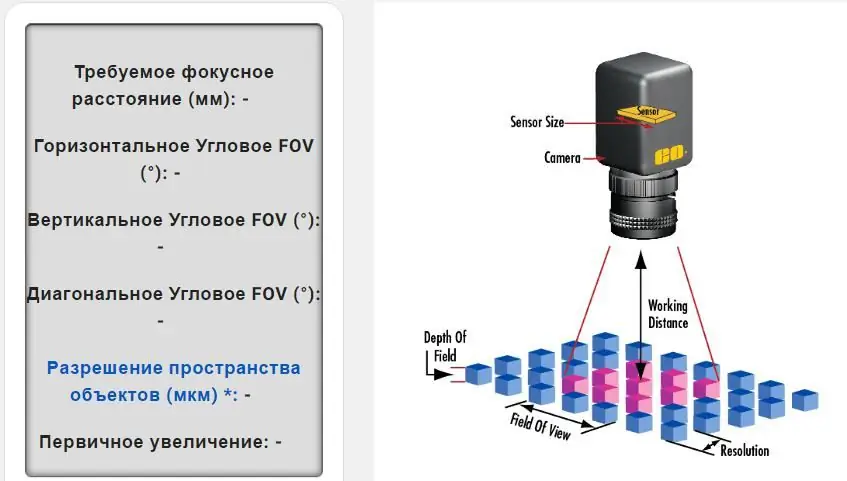
En realitat, aquests càlculs són força complexos, però us ajudaran a crear una imatge basada en la mida del sensor, el format de píxel, la distància de treball i el camp de visió en mm. El càlcul d'aquests valors determinarà la millor lent per a les vostres imatges i aplicació.
Problemes de l'òptica moderna

Malauradament, duplicar la mida del sensor crea problemes addicionals per a les lents. Un dels principals paràmetres que afecten el cost d'una lent d'imatge és el format. Dissenyar una lent per a un sensor de format més gran requereixnombrosos components òptics individuals, que haurien de ser més grans i la transferència del sistema més rígida.
Una lent dissenyada per a un sensor d'1" pot costar cinc vegades més que una lent dissenyada per a un sensor de ½", encara que no pugui utilitzar les mateixes especificacions amb una resolució de píxels limitada. El component de cost s'ha de considerar abans de com per determinar el poder de resolució d'una lent.
La imatge òptica avui s'enfronta a més reptes que fa una dècada. Els sensors amb els quals s'utilitzen tenen requisits de resolució molt més alts i les mides de format es fan simultàniament més petites i més grans, mentre que la mida dels píxels segueix reduint-se.
En el passat, l'òptica mai limitava el sistema d'imatge, avui ho fa. Quan una mida de píxel típica és d'uns 9 µm, una mida molt més habitual és d'uns 3 µm. Aquest augment de 81 vegades en la densitat de punts ha passat factura a l'òptica i, tot i que la majoria dels dispositius són bons, la selecció de lents és ara més important que mai.






