En física, s'estudia el tema de la connexió en paral·lel i en sèrie, i pot ser no només conductors, sinó també condensadors. Aquí és important no confondre's sobre com es veu cadascun d'ells al diagrama. I només llavors apliqueu fórmules específiques. Per cert, cal recordar-los de memòria.
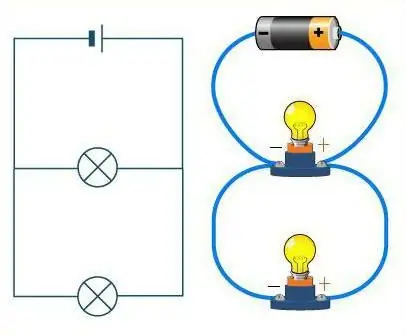
Com distingir entre aquests dos compostos?
Mireu de prop el diagrama. Si els cables es representen com una carretera, els cotxes que hi ha al seu interior faran el paper de resistències. Per un camí recte sense bifurcacions, els cotxes circulen un darrere l' altre, en cadena. La connexió en sèrie dels conductors també té el mateix aspecte. La carretera en aquest cas pot tenir un nombre il·limitat de girs, però no una sola intersecció. No importa com hagi mogut la carretera (cables), les màquines (resistències) sempre estaran situades una darrere l' altra, en una cadena.
Si es considera una connexió en paral·lel, és molt diferent. A continuació, les resistències es poden comparar amb els atletes a la sortida. Ells sóncadascun es troba en la seva pròpia pista, però tenen la mateixa direcció de moviment, i la meta és al mateix lloc. De la mateixa manera, les resistències: cadascuna d'elles té el seu propi cable, però totes estan connectades en algun moment.
Fórmules per a la força actual
Sempre es parla al tema "Electricitat". Les connexions en paral·lel i en sèrie afecten la quantitat de corrent a les resistències de diferents maneres. Per a ells, es deriven fórmules que es poden recordar. Però n'hi ha prou amb recordar el significat que s'hi inverteix.
Per tant, el corrent en connexió en sèrie dels conductors és sempre el mateix. És a dir, en cadascun d'ells el valor de la força actual no és diferent. Podeu fer una analogia si compareu un cable amb una canonada. En ell, l'aigua flueix sempre de la mateixa manera. I tots els obstacles al seu camí seran escombrats amb la mateixa força. El mateix amb el corrent. Per tant, la fórmula per al corrent total en un circuit amb una connexió en sèrie de resistències és així:
I gen=I 1=I 2
Aquí, la lletra I indica la força del corrent. Aquesta és una notació habitual, així que cal que la recordis.
El corrent en connexió en paral·lel ja no serà un valor constant. Amb la mateixa analogia amb una canonada, resulta que l'aigua es dividirà en dos corrents si la canonada principal té una branca. El mateix fenomen s'observa amb el corrent quan apareix una ramificació de cables al seu pas. La fórmula per a la intensitat total del corrent quan els conductors estan connectats en paral·lel:
I gen=I 1 + I 2
Si la ramificació està formada per cables quemés de dos, llavors a la fórmula anterior hi haurà més termes pel mateix nombre.
Fórmules per a l'estrès
Quan es considera un circuit en què els conductors estan connectats en sèrie, la tensió en tota la secció ve determinada per la suma d'aquests valors en cada resistència específica. Podeu comparar aquesta situació amb les plaques. Serà fàcil que una persona aguanti un d'ells, també podrà agafar el segon a prop, però amb dificultat. Una persona ja no podrà aguantar tres plats un al costat de l' altre, caldrà l'ajuda d'un segon. Etc. Els esforços de la gent sumen.
La fórmula per a la tensió total d'una secció d'un circuit amb una connexió en sèrie de conductors és així:
U gen=U 1 + U 2, on U és la designació adoptada per a la tensió elèctrica.
Si es considera una connexió paral·lela de resistències, sorgeix una altra situació. Quan els plats s'apilen uns sobre els altres, una persona encara els pot subjectar. Així que no cal afegir res. La mateixa analogia s'observa quan els conductors estan connectats en paral·lel. La tensió de cadascun d'ells és la mateixa i igual a la que hi ha a totes alhora. La fórmula per a la tensió total és:
U gen=U 1=U 2
Fórmules per a la resistència elèctrica
Ja no els pots memoritzar, però coneixes la fórmula de la llei d'Ohm i en deriva'n la desitjada. D'aquesta llei es dedueix quela tensió és igual al producte del corrent per la resistència. És a dir, U=IR, on R és la resistència.
Llavors, la fórmula amb la qual haureu de treballar depèn de com estiguin connectats els conductors:
- en sèrie, de manera que necessiteu la igu altat de tensió - IgenRtotal=I1R1 + I2R2;
- en paral·lel, cal utilitzar la fórmula per a la força actual - Utotal / Rtotal=U 1/ R1 + U2 / R2 .
Seguides de transformacions simples, que es basen en el fet que en la primera igu altat tots els corrents tenen el mateix valor, i en la segona - les tensions són iguals. Així es poden escurçar. És a dir, s'obtenen les expressions següents:
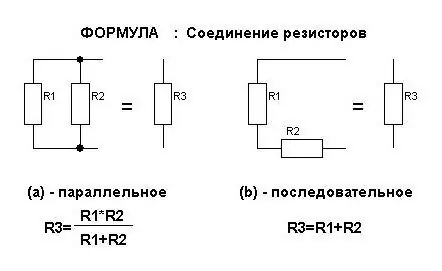
- R gen=R 1 + R 2 (per a la connexió en sèrie de conductors).
- 1/R gen=1/R 1 + 1/R 2(quan es connecta en paral·lel).
Quan augmenta el nombre de resistències connectades a la xarxa, el nombre de termes d'aquestes expressions canvia.
Val la pena assenyalar que la connexió en paral·lel i en sèrie dels conductors té un efecte diferent sobre la resistència total. El primer d'ells redueix la resistència de la secció del circuit. A més, resulta ser inferior a la més petita de les resistències utilitzades. Quan es connecta en sèrie, tot és lògic: els valors se sumen, de manera que el nombre total sempre serà el més gran.
Corrent de treball
Les tres magnituds anteriors conformen les lleis de la connexió en paral·lel i la disposició en sèrie dels conductors d'un circuit. Per tant, és imprescindible conèixer-los. Sobre el treball i el poder, només cal recordar la fórmula bàsica. S'escriu de la següent manera: A \u003d IUt, on A és el treball del corrent, t és el temps del seu pas pel conductor.
Per determinar el treball total amb una connexió en sèrie, cal substituir la tensió a l'expressió original. S'obté la igu altat: A \u003d I(U 1 + U 2)t, obrint els claudàtors en què resulta que el el treball a tota la secció és igual a la quantitat de cada consumidor actual específic.
El raonament procedeix de la mateixa manera si es considera un esquema de connexió paral·lel. Només s'ha de substituir la força actual. Però el resultat serà el mateix: A=A 1 + A 2.
Potència actual
Quan es deriva una fórmula per a la potència (notació "P") d'una secció de circuit, cal que torneu a utilitzar una fórmula: P \u003d UI. Després d'aquest raonament, resulta que les connexions en paral·lel i en sèrie són descrit per aquesta fórmula per al poder: P \u003d P1 + P 2.
És a dir, sigui com s'elaborin els esquemes, la potència total serà la suma dels implicats en l'obra. Això explica el fet que és impossible incloure molts dispositius potents a la xarxa d'apartaments alhora. Simplement no pot agafar la càrrega.
Com afecta la connexió dels conductors a la reparació de la garlanda de Cap d'Any?
Immediatament després que una de les bombetes s'hagi cremat, queda clar com estaven connectades. A lesconnexió en sèrie, cap d'ells s'il·luminarà. Això es deu al fet que una làmpada que s'ha tornat inutilitzable crea una ruptura en el circuit. Per tant, heu de comprovar-ho tot per determinar quin s'ha cremat, substituir-lo i la garlanda començarà a funcionar.
Si utilitza una connexió paral·lela, no deixarà de funcionar si falla una de les bombetes. Després de tot, la cadena no es trencarà completament, sinó només una part paral·lela. Per reparar aquesta garlanda, no cal que comproveu tots els elements del circuit, sinó només els que no brillen.
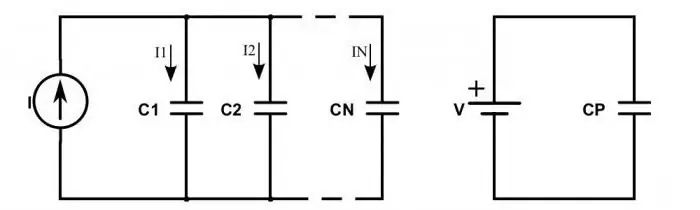
Què passa amb un circuit si s'inclouen condensadors en comptes de resistències?
Quan estan connectats en sèrie, s'observa la següent situació: les càrregues dels avantatges de la font d'alimentació només arriben a les plaques exteriors dels condensadors extrems. Els que hi ha entremig simplement passen aquesta càrrega al llarg de la cadena. Això explica el fet que a totes les plaques apareguin les mateixes càrregues, però amb signes diferents. Per tant, la càrrega elèctrica de cada condensador connectat en sèrie es pot escriure de la següent manera:
q gen =q 1=q 2.
Per determinar la tensió de cada condensador, haureu de conèixer la fórmula: U=q / C. En ella, C és la capacitat del condensador.
La tensió total segueix la mateixa llei que les resistències. Per tant, substituint la tensió a la fórmula de la capacitat per la suma, obtenim que la capacitat total dels dispositius s'ha de calcular mitjançant la fórmula:
C=q / (U 1 + U2).
Podeu simplificar aquesta fórmula invertint les fraccions i substituint la relació de voltatge a càrrega per capacitat. Resulta la següent igu altat: 1 / С=1 / С 1 + 1 / С 2.
La situació sembla una mica diferent quan els condensadors estan connectats en paral·lel. Aleshores, la càrrega total es determina per la suma de totes les càrregues que s'acumulen a les plaques de tots els dispositius. I el valor de la tensió encara es determina segons les lleis generals. Per tant, la fórmula per a la capacitat total dels condensadors connectats en paral·lel és:
С=(q 1 + q 2) / U.
És a dir, aquest valor es considera com la suma de cadascun dels dispositius utilitzats a la connexió:
S=S 1 + S 2.
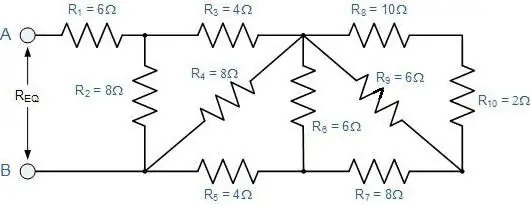
Com determinar la resistència total d'una connexió arbitrària de conductors?
És a dir, aquell en què les seccions successives substitueixen les paral·leles, i viceversa. Per a ells, totes les lleis descrites encara són vàlides. Només cal que els apliqueu per etapes.
Primer, se suposa que ha d'ampliar mentalment l'esquema. Si és difícil imaginar-ho, cal dibuixar què passa. L'explicació serà més clara si la considerem amb un exemple concret (vegeu la figura).
És convenient començar a dibuixar des dels punts B i C. S'han de col·locar a certa distància l'un de l' altre i de les vores del full. A l'esquerra, un cable s'acosta al punt B i dos ja estan dirigits a la dreta. El punt B, en canvi, té dues branques a l'esquerra i un cable després.
Ara heu d'omplir l'espai entre aquestspunts. Al llarg del cable superior s'han de col·locar tres resistències amb coeficients de 2, 3 i 4, i des de baix anirà la que té un índex de 5. Les tres primeres estan connectades en sèrie. Amb la cinquena resistència estan en paral·lel.
Les dues resistències restants (la primera i la sisena) estan connectades en sèrie amb la secció considerada de la BV. Per tant, el dibuix es pot complementar simplement amb dos rectangles a banda i banda dels punts seleccionats. Queda per aplicar les fórmules per calcular la resistència:
- primer el donat per a la connexió en sèrie;
- després per a paral·lel;
- i una altra vegada consecutives.
D'aquesta manera, podeu implementar qualsevol esquema, fins i tot molt complex.
El problema de la connexió en sèrie dels conductors
Condició. Dues làmpades i una resistència estan connectades en un circuit una darrere l' altra. La tensió total és de 110 V i el corrent és de 12 A. Quin és el valor de la resistència si cada làmpada té 40 V?
Decisió. Com que s'està considerant una connexió en sèrie, es coneixen les fórmules de les seves lleis. Només cal aplicar-los correctament. Comenceu per esbrinar el valor de voltatge a través de la resistència. Per fer-ho, cal restar dues vegades la tensió d'una làmpada del total. Resulta que 30 V.
Ara que es coneixen dues magnituds, U i I (la segona d'elles es dóna en la condició, ja que el corrent total és igual al corrent de cada consumidor en sèrie), podem calcular la resistència de la resistència utilitzant la llei d'Ohm. Resulta que és de 2,5 ohms.
Resposta. La resistència de la resistència és de 2,5 ohms.
Tascaper a la connexió de condensadors, en paral·lel i en sèrie
Condició. Hi ha tres condensadors amb capacitats de 20, 25 i 30 microfarads. Determineu la seva capacitat total quan es connecten en sèrie i en paral·lel.
Decisió. És més fàcil començar amb una connexió en paral·lel. En aquesta situació, només cal afegir els tres valors. Per tant, la capacitat total és de 75 uF.
Els càlculs seran una mica més complicats quan aquests condensadors estiguin connectats en sèrie. Després de tot, primer heu de trobar la proporció d'unitat a cadascuna d'aquestes capacitats i després afegir-les entre elles. Resulta que la unitat dividida per la capacitat total és 37/300. Aleshores, el valor desitjat és d'aproximadament 8 microfarads.
Resposta. La capacitat total en connexió en sèrie és de 8 uF, en paral·lel - 75 uF.






