Quan s'estudia física a 10è, es considera el tema dels dipols. Què significa aquest concepte i quines fórmules s'utilitzen per calcular-lo?
Introducció
Si col·loqueu un dipol a l'espai d'un camp elèctric uniforme, podeu representar-lo com a línies de força. Un dipol és un sistema en què hi ha dues càrregues que són idèntiques en paràmetres, però són càrregues puntuals oposades. A més, la distància entre ells serà molt menor que la distància a qualsevol punt del camp dipolar. El concepte de moment dipolar s'estudia al curs escolar d'electrodinàmica (10è grau).
L'eix del dipol és una recta que passa pels punts d'ambdues càrregues. Un braç dipolar és un vector que connecta una càrrega i al mateix temps passa de partícules carregades negativament a partícules carregades positivament. Un dipol elèctric es caracteritza per la presència d'un estat com un dipol o moment elèctric.
Per definició, un moment dipolar és un vector numèricament igual al producte de la càrrega dipolar i el seu braç. A més, està codirigit amb l'espatlla del dipol. A la igu altat zero de la suma de forces, calculem el valor del moment. Per a l'angle que hi ha entre el moment dipolar idireccionalitat del camp elèctric, la presència d'un moment mecànic és característica.
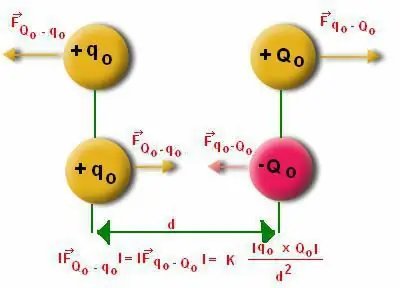
Sovint a la gent li costa calcular el mòdul que actua sobre l'estructura del dipol. Aquí cal tenir en compte les peculiaritats del càlcul de l'angle "Alfa". Se sap que el dipol es desvia de la posició d'equilibri. Però el mateix moment dipolar té un caràcter restaurador, ja que tendeix a estar en moviment.
Càlculs
Quan aquest moment dipolar es col·loca en el medi d'un camp elèctric no homogeni, inevitablement sorgeix una força. En aquest entorn, els indicadors de la suma de forces no seran zero. En conseqüència, hi ha forces que actuen sobre el moment dipolar amb caràcter puntual. La mida del braç del dipol és molt més petita.
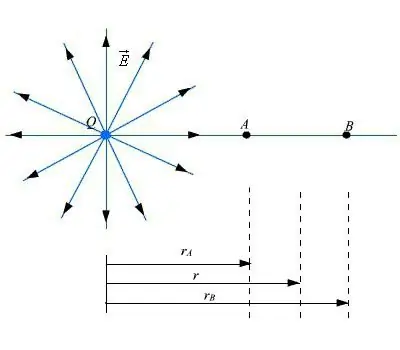
La fórmula es pot escriure així: F=q (E2 - E1)=qdE, on d és el diferencial del camp elèctric.
Cerca les característiques del concepte físic en estudi
Mirem el tema més enllà. Per determinar quina és la característica del camp elèctric, si es crea mitjançant un sistema de càrregues i es localitza en un espai reduït, cal fer una sèrie de càlculs. Un exemple el presenten els àtoms i les molècules, que en la seva composició tenen nuclis i electrons carregats elèctricament.
Si cal buscar un camp a una distància superior a les dimensions que conformen la zona on es troben les partícules, utilitzarem una sèrie de fórmules exactes i molt complexes. És possible utilitzar-lo més senzillexpressions aproximades. Suposem que els conjunts puntuals de càrregues qk participen en la creació del camp elèctric. Es troben en un espai reduït.
Per realitzar el càlcul de la característica que té el camp, es permet combinar totes les càrregues del sistema. Aquest sistema es considera una càrrega puntual Q. Els indicadors de magnitud seran la suma de les càrregues que hi havia al sistema original.
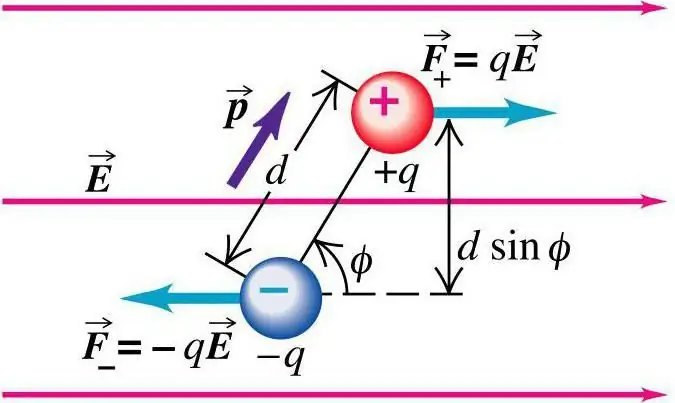
Ubicació dels càrrecs
Imaginem que la ubicació del càrrec s'indica en qualsevol lloc on es trobi el sistema de càrrecs qk. En fer canvis a la ubicació, si té límits expressats en una àrea petita, aquesta influència serà insignificant, gairebé imperceptible per al camp des del punt de vista. Dins dels límits d'aproximació de força i potencial que té el camp elèctric, les determinacions es fan mitjançant fórmules tradicionals.
Quan la suma de la càrrega total del sistema és zero, els paràmetres de l'aproximació indicada es veuran aproximats. Això dóna motius per concloure que el camp elèctric simplement està absent. Si cal obtenir una aproximació més precisa, recull mentalment grups separats de càrregues positives i negatives del sistema que s'està considerant.
En el cas del desplaçament dels seus "centres" respecte d' altres, els paràmetres de camp en aquest sistema es poden descriure com un camp que té dues càrregues puntuals, iguals en magnitud i oposades en signe. S'observa que estan desplaçats en relació als altres. ProveirPer a una caracterització més precisa del sistema de càrregues pel que fa als paràmetres d'aquesta aproximació, caldrà estudiar les propietats d'un dipol en un camp elèctric.
Introducció del terme
Tornem a la definició. Un dipol elèctric és la definició d'un sistema que té dues càrregues puntuals. Tenen la mateixa mida i signes oposats. A més, aquests senyals es troben a petites distàncies en relació amb altres senyals.
Es pot calcular la característica del procés que es crea mitjançant un dipol, i es representa amb dues càrregues puntuals: +q i −q, i es troben a una distància a relativa a les altres.

Seqüència de càlculs
Comencem calculant el potencial i la intensitat que té el dipol a la seva superfície axial. Aquesta és una línia recta que transcorre entre dues càrregues. Sempre que el punt A estigui situat a una distància igual a r respecte a la part central del dipol, i si és r >> a, segons el principi de superposició del potencial de camp en aquest punt, serà racional utilitza l'expressió per calcular els paràmetres del dipol elèctric.
La magnitud del vector de força es calcula pel principi de superposició. Per calcular la intensitat de camp, s'utilitza el concepte de la relació entre potencial i intensitat de camp:
Ex=−Δφ /Δx.
En aquestes condicions, la direcció del vector d'intensitat s'indica longitudinalment en relació amb l'eix del dipol. Per calcular el seu mòdul, s'aplica la fórmula estàndard.
Importantaclariments
S'ha de tenir en compte que el debilitament del camp dipolar elèctric es produeix més ràpidament que no pas una càrrega puntual. La decadència del potencial de camp dipolar és inversament proporcional al quadrat de la distància, i la intensitat del camp és inversament proporcional al cub de la distància.
Usant mètodes similars, però més complicats, els paràmetres del potencial i la intensitat de camp del dipol es troben en punts arbitraris, els paràmetres de posició dels quals es determinen mitjançant un mètode de càlcul com les coordenades polars: la distància a la centre del dipol elèctric (r) i l'angle (θ).
Càlcul mitjançant el vector de tensió
El concepte del vector intensitat E es divideix en dos punts:
- Radial (Er), que es dirigeix en la direcció longitudinal respecte a la línia recta.
- Aquesta línia recta connecta el punt especificat i el centre del dipol amb la perpendicular a aquest Eθ.
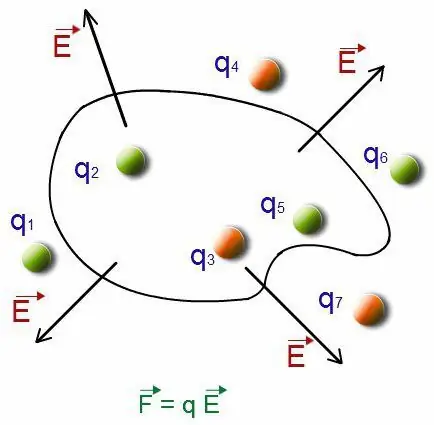
Aquesta descomposició de cada component es dirigeix al llarg del curs del canvi que es produeix amb totes les coordenades del punt a observar. El podeu trobar per la relació que relaciona els indicadors d'intensitat de camp amb possibles modificacions.
Trobant el component vectorial a la intensitat del camp, és important establir la naturalesa de la relació en els canvis potencials que es produeixen a causa del desplaçament del punt d'observació en la direcció dels vectors.
Calculeu la component perpendicular
Quan hagi acabatPer a aquest procediment, és important tenir en compte que l'expressió de la magnitud a un petit desplaçament perpendicular es determinarà canviant l'angle: Δl=rΔθ. Els paràmetres de magnitud d'aquest component de camp seran iguals.
Un cop obtinguda la relació, és possible determinar el camp del dipol elèctric en un punt arbitrari per construir una imatge amb les línies de força d'aquest camp.
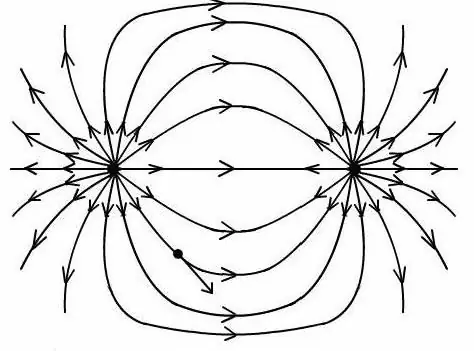
És important tenir en compte que totes les fórmules per determinar el potencial i la intensitat de camp d'un dipol funcionen només en el producte dels valors que té una càrrega dipol i la distància entre elles.
Moment dipolar
El títol de l'obra descrita és una descripció completa del tipus elèctric de propietats. Té el nom de "moment dipolar del sistema".
Per definició de dipol, que és un sistema de càrregues puntuals, es pot esbrinar que es caracteritza per la presència de simetria axial, quan l'eix és una recta que passa per diverses càrregues.
Per establir la característica completa del dipol, indiqueu la direcció d'orientació que té l'eix. Per simplificar els càlculs, es pot especificar el vector del moment dipolar. El valor de la seva magnitud és igual a la magnitud del moment dipolar, i el vector de direcció difereix per la coincidència d'aquest i l'eix del dipol. Per tant, p=qa si a és la direcció del vector que connecta les càrregues negatives i positives del dipol.
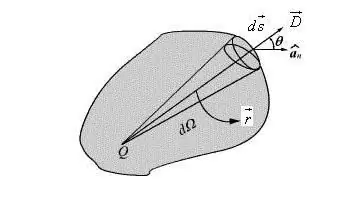
L'ús d'aquesta característica del dipol és convenient i permet en la majoria dels casos simplificar la fórmula i donar-li la formavector. La descripció del potencial del camp dipolar en un punt d'una direcció arbitrària s'escriu en forma de vector.
La introducció de conceptes com la característica vectorial d'un dipol i el seu moment dipolar es pot realitzar mitjançant un model simplificat: una càrrega puntual en un camp uniforme, que inclou un sistema de càrregues, les dimensions geomètriques de les quals no no s'ha de tenir en compte, però és important conèixer el moment dipolar. Aquest és un requisit previ per fer càlculs.
Com es comporta un dipol
El comportament d'un dipol es pot veure en l'exemple d'aquesta situació. La posició de dues càrregues puntuals té un caràcter fix de distància entre si. Es van col·locar en les condicions d'un dipol d'un camp elèctric uniforme. Fes observacions sobre el procés. A les lliçons de física (electrodinàmica), aquest concepte es considera amb detall. Des del camp fins a la càrrega, es realitza l'acció de les forces:
F=±qE
Són de la mateixa magnitud i de direcció oposada. L'indicador de la força total que actua sobre el dipol és zero. Com que aquesta força té un efecte en diversos punts, el moment total serà:
M=Fa sin a=qEa sin a=pE sin a, sent α l'angle que connecta els vectors d'intensitat de camp i els vectors de moment dipolar. A causa de la presència d'un moment de força, el moment dipolar del sistema tendeix a tornar a les direccions del vector d'intensitat del camp elèctric.
El dipol elèctric és un concepte que és important entendre amb claredat. Podeu llegir-ne més informació a Internet. També potper estudiar a les lliçons de física a l'escola a 10è grau, com hem parlat més amunt.






