Els fenòmens i processos naturals que ens envolten són força complexos. Per a la seva descripció física exacta, s'hauria d'utilitzar un aparell matemàtic feixuc i s'hauria de tenir en compte un gran nombre de factors significatius. Per evitar aquest problema, s'utilitzen alguns models simplificats en física, que faciliten molt l'anàlisi matemàtica del procés, però pràcticament no afecten la precisió de la seva descripció. Un d'ells és el model de gas ideal. Considerem-ho amb més detall a l'article.
El concepte de gas ideal
Un gas ideal és un estat d'agregació d'una substància, que consta de punts materials que no interaccionen entre ells. Expliquem aquesta definició amb més detall.
Primer, estem parlant de punts materials com a objectes que formen un gas ideal. Això vol dir que les seves molècules i àtoms no tenen una mida, sinó que tenen una massa determinada. És atrevites pot fer una aproximació tenint en compte el fet que en tots els gasos reals a baixes pressions i altes temperatures, la distància entre molècules és molt més gran que les seves dimensions lineals.
En segon lloc, les molècules d'un gas ideal no haurien d'interaccionar entre elles. En realitat, aquestes interaccions sempre existeixen. Així, fins i tot els àtoms de gasos nobles experimenten atracció dipol-dipol. En altres paraules, les interaccions de van der Waals estan presents. Tanmateix, en comparació amb l'energia cinètica de rotació i el moviment de translació de les molècules, aquestes interaccions són tan petites que no afecten les propietats dels gasos. Per tant, no es poden tenir en compte a l'hora de resoldre problemes pràctics.
És important tenir en compte que no tots els gasos en els quals la densitat és baixa i la temperatura és alta es poden considerar ideals. A més de les interaccions de van der Waals, hi ha altres tipus d'enllaços més forts, per exemple, els enllaços d'hidrogen entre les molècules H2O, que condueixen a una violació greu de les condicions d'idealitat del gas. Per aquest motiu, el vapor d'aigua no és un gas ideal, sinó l'aire.
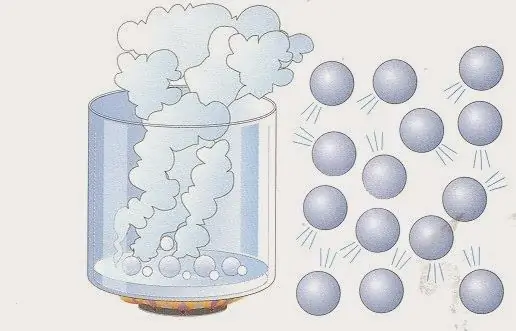
Model físic d'un gas ideal
Aquest model es pot representar de la següent manera: suposem que el sistema de gas conté N partícules. Aquests poden ser àtoms i molècules de diversos productes químics i elements. El nombre de partícules N és gran, per la qual cosa s'acostuma a utilitzar la unitat "mol" per descriure-ho (1 mol correspon al nombre d'Avogadro). Tots es mouen en algun volum V. Moviments de partículessón caòtics i independents els uns dels altres. Cadascun d'ells té una certa velocitat v i es mou per un camí recte.
Teòricament, la probabilitat de col·lisió entre partícules és gairebé nul·la, ja que la seva mida és petita en comparació amb les distàncies entre partícules. Tanmateix, si es produeix una col·lisió així, és absolutament elàstica. En aquest últim cas, es conserva el moment total de les partícules i la seva energia cinètica.
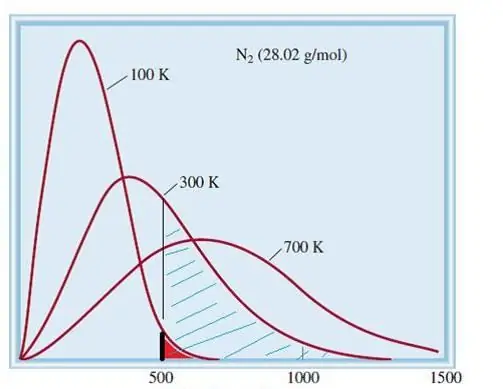
El model considerat de gasos ideals és un sistema clàssic amb un gran nombre d'elements. Per tant, la velocitat i l'energia de les partícules en ella obeeixen a la distribució estadística de Maxwell-Boltzmann. Algunes partícules tenen velocitats baixes, mentre que altres tenen velocitats elevades. En aquest cas, hi ha un cert límit de velocitat estret, en el qual es troben els valors més probables d'aquesta quantitat. La distribució de velocitats de les molècules de nitrogen es mostra esquemàticament a continuació.
Teoria cinètica dels gasos
El model de gasos ideals descrit anteriorment determina de manera única les propietats dels gasos. Aquest model va ser proposat per primera vegada per Daniel Bernoulli el 1738.

Posteriorment, va ser desenvolupat fins al seu estat actual per August Kroenig, Rudolf Clausius, Mikhail Lomonosov, James Maxwell, Ludwig Boltzmann, Marian Smoluchowski i altres científics.
La teoria cinètica de les substàncies fluides, sobre la base de la qual es construeix el model de gas ideal, explica dues propietats macroscòpiques importants del sistema en funció del seu comportament microscòpic:
- La pressió dels gasos és el resultat de la col·lisió de partícules amb les parets del recipient.
- La temperatura del sistema és el resultat de la manifestació del moviment constant de molècules i àtoms.
Ampliem les dues conclusions de la teoria cinètica.
Pressió del gas
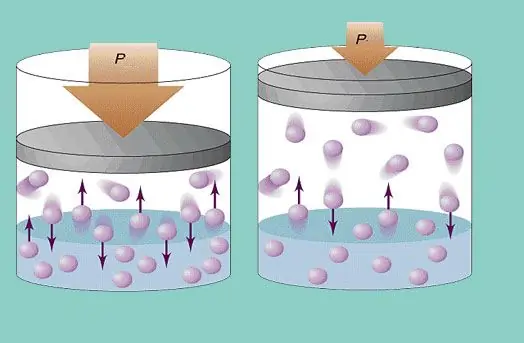
El model de gas ideal suposa un moviment caòtic constant de partícules en el sistema i la seva col·lisió constant amb les parets del vaixell. Cada cop d'aquest tipus es considera absolutament elàstic. La massa de la partícula és petita (≈10-27-10-25 kg). Per tant, no pot crear molta pressió en una col·lisió. No obstant això, el nombre de partícules, i per tant el nombre de col·lisions, és enorme (≈1023). A més, la velocitat quadrada mitjana dels elements és de diversos centenars de metres per segon a temperatura ambient. Tot això comporta la creació d'una pressió apreciable a les parets del vaixell. Es pot calcular amb la fórmula següent:
P=Nmvcp2 / (3V), on vcp és la velocitat quadrada mitjana, m és la massa de partícules.
Temperatura absoluta
Segons el model de gas ideal, la temperatura està determinada exclusivament per l'energia cinètica mitjana d'una molècula o àtom del sistema en estudi. Podeu escriure l'expressió següent que relaciona l'energia cinètica i la temperatura absoluta d'un gas ideal:
mvcp2 / 2=3/2kB T.
Aquí kB és la constant de Boltzmann. D'aquesta igu altat obtenim:
T=m vcp2 / (3kB).
Equació d'estat universal
Si combinem les expressions anteriors per a la pressió absoluta P i la temperatura absoluta T, podem escriure la igu altat següent:
PV=nRT.
Aquí n és la quantitat de substància en mols, R és la constant de gas introduïda per D. I. Mendeleiev. Aquesta expressió és l'equació més important en la teoria dels gasos ideals, perquè combina tres paràmetres termodinàmics (V, P, T) i no depèn de les característiques químiques del sistema de gasos.

L'equació universal va ser derivada per primera vegada experimentalment pel físic francès Emile Clapeyron al segle XIX i després portada a la seva forma moderna pel químic rus Mendeleiev, motiu pel qual actualment porta els noms d'aquests científics.






