La piràmide juntament amb un prisma és un poliedre perfecte en l'espai tridimensional, les seves característiques geomètriques s'estudien a l'institut. En aquest article, analitzarem què són les piràmides, en quins elements consten, i també caracteritzarem breument les piràmides correctes.
Piràmide de figures geomètriques
Des del punt de vista de la geometria, la piràmide és una figura espacial, formada per un polígon i diversos triangles. Obtenir aquesta figura és bastant senzill. Per fer-ho, agafeu un polígon amb n costats, trieu un punt arbitrari de l'espai que no estigui en el pla del polígon i connecteu cada vèrtex del polígon amb aquest punt. Òbviament, la figura formada d'aquesta manera tindrà n triangles connectats entre si en un vèrtex.
Per visualitzar la forma geomètrica de la figura descrita, fem una foto.

Això mostra una piràmide quadrangular, la base de la qual ésquadrilàter, i la superfície lateral està formada per quatre triangles que tenen un vèrtex comú.
Elements de la piràmide
Com qualsevol poliedre, la piràmide està formada per tres tipus d'elements:
- vores;
- tops;
- costelles.
Les cares són parts de plans que separen el volum intern d'una figura de l'espai circumdant. Si la base de la piràmide conté un n-gon, aleshores el nombre de les seves cares és sempre n+1. D'aquests, n costats són triangulars i un costat és la base n-gonal esmentada.
Els vèrtexs són punts on es tallen tres o més cares d'una figura. La regió base conté n vèrtexs, cadascun dels quals està format per dues cares triangulars i una base. El punt on es troben n costats triangulars s'anomena la part superior de la piràmide. Per tant, la figura considerada consta de n+1 vèrtexs.
Les arestes són línies rectes que apareixen quan dues cares es tallen. Cada aresta està limitada per dos vèrtexs als seus extrems. Qualsevol piràmide amb una base n-gon conté 2n arestes. La meitat d'aquest nombre, és a dir, n, està format únicament per la intersecció de triangles laterals.
Possibles tipus de xifres
El nom de la figura considerada està determinat exclusivament pel tipus de polígon a la base. Per exemple, si té tres cantonades i tres costats, aleshores la piràmide serà triangular, si és quatre - quadrangular, i així successivament.
El polígon pot ser convex i còncau, així com regular i general. Tot això també determina l'aparició de la piràmide.
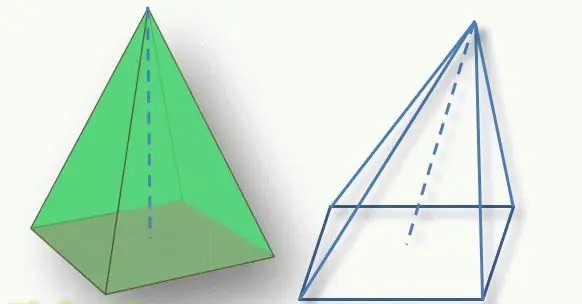
Un punt important per determinar el tipus de figura és la posició de la part superior de la piràmide respecte a la seva base. El segment perpendicular dibuixat des de la part superior fins a la base poligonal s'anomena alçada de la figura. Si aquest segment talla la base en el seu centre geomètric (per a un triangle, aquesta és la intersecció de mitjanes, per a un quadrilàter, la intersecció de diagonals), aleshores la figura s'anomena recta. En cas contrari, parlen d'una piràmide inclinada.
Si l'n-gon de la base és regular (triangle equilàter, quadrat, etc.) i la figura és recta, llavors s'anomena piràmide regular.
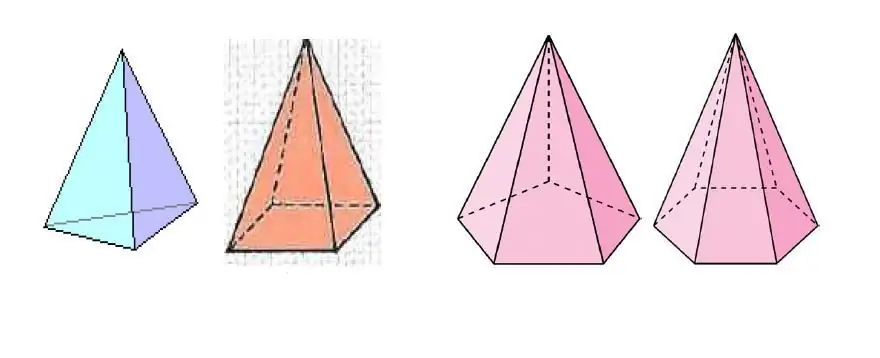
La imatge de d alt mostra diverses piràmides, que es diferencien pel nombre de costats del polígon a la base.
Propietats de les piràmides regulars
Aquestes piràmides es diferencien d' altres figures d'aquesta classe per un alt grau de simetria. En aquest sentit, és convenient realitzar diversos càlculs geomètrics amb ells, per exemple, volum o superfície.
Una piràmide regular conté un n-gon a la seva base, l'àrea de la qual es determina de manera única a partir del coneixement de la longitud del seu costat. La superfície lateral de la figura està formada per n triangles idèntics, que són equilàters. Les vores d'una piràmide regular situada a la superfície lateral són iguals entre si. El valor de la longitud d'aquesta vora s'utilitza sovint quan es calcula l'apotema d'una figura i es determina la superfície.
L'alçada d'una piràmide regular és la segona característica important de la figura (la primera és la longitud de la voramotius). L'alçada s'utilitza per calcular el volum.
Qualsevol pla paral·lel a la base, que talla les cares laterals de la piràmide, condueix a la formació d'una secció poligonal. És homotètic respecte al polígon base. L'operació de tall descrita condueix a la formació de tota una classe de noves figures: piràmides regulars truncades.
Les piràmides més famoses

Per descomptat, aquestes són les piràmides quadrangulars regulars dels faraons egipcis. En un lloc anomenat Gizeh, hi ha més de 100 d'aquests monuments de pedra, la perfecció del disseny i la precisió dels paràmetres geomètrics dels quals continuen sorprès els científics fins avui. La més gran d'elles és la piràmide de Keops, que té uns 146 metres d'alçada i uns 230 metres de llarg.
Per a què van servir exactament aquestes piràmides, així com amb quins mecanismes i quan es van construir, ningú sap fins avui.






