Estudiar els processos que ocorren en sistemes estadístics és complicat per la mida mínima de les partícules i el seu gran nombre. És pràcticament impossible considerar cada partícula per separat, per tant, s'introdueixen quantitats estadístiques: la velocitat mitjana de les partícules, la seva concentració, la massa de la partícula. La fórmula que caracteritza l'estat del sistema, tenint en compte els paràmetres microscòpics, s'anomena equació bàsica de la teoria cinètica molecular dels gasos (MKT).
Una mica sobre la velocitat mitjana de les partícules
La determinació de la velocitat de les partícules es va dur a terme primer experimentalment. Un conegut experiment del currículum escolar, realitzat per Otto Stern, va permetre crear una idea de les velocitats de les partícules. Durant l'experiment es va estudiar el moviment dels àtoms de plata en cilindres giratoris: primer, en estat estacionari de la instal·lació, després quan girava amb una certa velocitat angular.
Com a resultat, es va trobar que la velocitat de les molècules de plata supera la velocitat del so i és de 500 m/s. El fet és força interessant, ja que és difícil que una persona senti aquestes velocitats de moviment de partícules en substàncies.
Gasolina ideal
Continua la recercaSembla possible només en un sistema els paràmetres del qual es poden determinar mitjançant mesures directes utilitzant instruments físics. La velocitat es mesura amb un velocímetre, però la idea de connectar un velocímetre a una sola partícula és absurda. Només es pot mesurar directament un paràmetre macroscòpic associat al moviment de partícules.
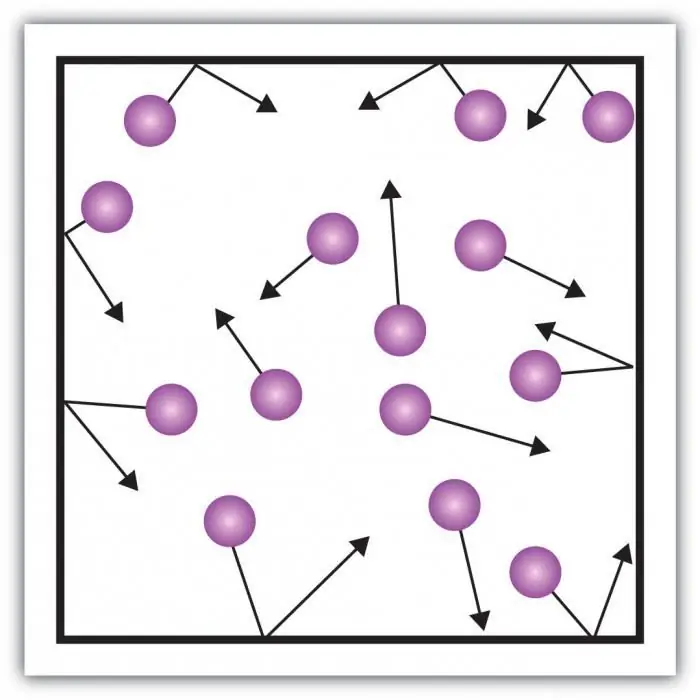
Considereu la pressió del gas. La pressió sobre les parets del recipient es crea pels impactes de les molècules del gas del recipient. La particularitat de l'estat gasós de la matèria es troba en distàncies prou grans entre les partícules i la seva petita interacció entre elles. Això us permet mesurar directament la seva pressió.
Qualsevol sistema de cossos que interactuen es caracteritza per l'energia potencial i l'energia cinètica del moviment. El gas real és un sistema complex. La variabilitat de l'energia potencial no es presta a la sistematització. El problema es pot resoldre introduint un model que tingui les propietats característiques del gas, deixant de banda la complexitat de la interacció.
El gas ideal és un estat de la matèria en què la interacció de les partícules és insignificant, l'energia potencial d'interacció tendeix a zero. Només l'energia del moviment, que depèn de la velocitat de les partícules, es pot considerar significativa.
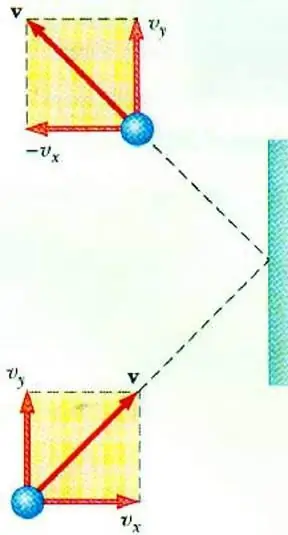
Pressió de gas ideal
Revelar la relació entre la pressió del gas i la velocitat de les seves partícules permet l'equació bàsica del MKT d'un gas ideal. Una partícula que es mou en un vaixell, en impactar amb la paret, li transfereix un impuls, el valor del qual es pot determinar a partir de la segona llei. Newton:
F∆t=2m0vx
El canvi en l'impuls d'una partícula durant l'impacte elàstic està associat a un canvi en la component horitzontal de la seva velocitat. F és la força que actua des del costat de la partícula sobre la paret durant un breu temps t; m0 - massa de partícules.
Totes les partícules de gas xoquen amb la superfície de l'àrea S durant el temps ∆t, movent-se en la direcció de la superfície amb velocitat vx i situades en un cilindre de volum Sυ x Δt. A la concentració de partícules n, exactament la meitat de les molècules es mou cap a la paret, l' altra meitat es mou en sentit contrari.
Un cop considerat la col·lisió de totes les partícules, podem escriure la llei de Newton per a la força que actua sobre l'àrea:
F∆t=nm0vx2S∆t
Com que la pressió del gas es defineix com la relació entre la força que actua perpendicularment a la superfície i l'àrea d'aquesta última, podem escriure:
p=F: S=nm0vx2
La relació resultant com a equació bàsica del MKT no pot descriure tot el sistema, ja que només es considera una direcció de moviment.
Distribució Maxwell
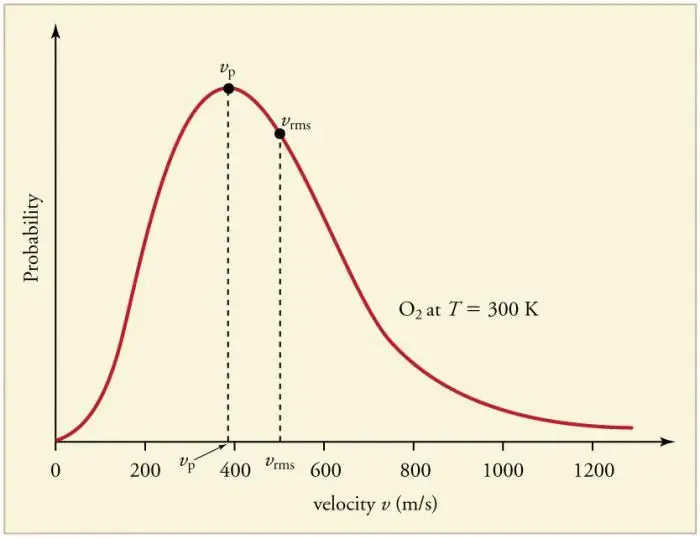
Les col·lisions freqüents i contínues de partícules de gas amb les parets i entre elles porten a l'establiment d'una certa distribució estadística de les partícules en termes de velocitats (energies). Les direccions de tots els vectors velocitat resulten ser igualment probables. Aquesta distribució s'anomena distribució de Maxwell. El 1860 aquest patró eraderivat per J. Maxwell sobre la base del MKT. Els principals paràmetres de la llei de distribució s'anomenen velocitats: probables, corresponents al valor màxim de la corba, i arrel quadrada mitjana vkv=√‹v2 › - el quadrat mitjà de la velocitat de la partícula.
L'augment de la temperatura del gas correspon a l'augment de la velocitat.
A partir del fet que totes les velocitats són iguals i els seus mòduls tenen el mateix valor, podem suposar:
‹v2›=‹vx2› + ‹v y2› + ‹vz2›, de: ‹ vx2›=‹v2›: 3
L'equació bàsica del MKT, tenint en compte el valor mitjà de la pressió del gas, és:
p=nm0‹v2›: 3.
Aquesta relació és única perquè determina la relació entre paràmetres microscòpics: velocitat, massa de partícules, concentració de partícules i pressió del gas en general.
Usant el concepte de l'energia cinètica de les partícules, l'equació bàsica del MKT es pot reescriure de manera diferent:
p=2nm0‹v2›: 6=2n‹Ek›: 3
La pressió d'un gas és proporcional al valor mitjà de l'energia cinètica de les seves partícules.
Temperatura
Curiosament, per a una quantitat constant de gas en un recipient tancat, es pot relacionar la pressió del gas i el valor mitjà de l'energia del moviment de les partícules. En aquest cas, la pressió es pot mesurar mesurant l'energiapartícules.
Què cal fer? Quin valor es pot comparar amb l'energia cinètica? La temperatura resulta ser aquest valor.

La temperatura és una mesura de l'estat tèrmic de les substàncies. Per mesurar-lo, s'utilitza un termòmetre, la base del qual és l'expansió tèrmica del fluid de treball (alcohol, mercuri) quan s'escalfa. L'escala del termòmetre es crea experimentalment. Normalment, s'hi col·loquen marques corresponents a la posició del fluid de treball durant algun procés físic que es produeix en un estat tèrmic constant (aigua bullint, gel en fusió). Els diferents termòmetres tenen diferents escales. Per exemple, Celsius, Fahrenheit.

Escala de temperatura universal
Els termòmetres de gas es poden considerar més interessants pel que fa a la independència de les propietats del fluid de treball. La seva escala no depèn del tipus de gas utilitzat. En aquest dispositiu, es pot identificar hipotèticament la temperatura a la qual la pressió del gas tendeix a zero. Els càlculs mostren que aquest valor correspon a -273,15 oC. L'escala de temperatura (escala de temperatura absoluta o escala Kelvin) es va introduir el 1848. La possible temperatura de pressió de gas zero es va prendre com a punt principal d'aquesta escala. Un segment d'unitat de l'escala és igual a un valor unitari de l'escala Celsius. Sembla més convenient escriure l'equació bàsica de MKT utilitzant la temperatura quan s'estudien els processos de gas.
Relació entre pressió i temperatura
Empíricament, podeu verificar-hoproporcionalitat de la pressió del gas a la seva temperatura. Al mateix temps, es va trobar que la pressió és directament proporcional a la concentració de partícules:
P=nkT,
on T és la temperatura absoluta, k és una constant igual a 1,38•10-23J/K.
El valor fonamental, que té un valor constant per a tots els gasos, s'anomena constant de Boltzmann.
Comparant la dependència de la pressió de la temperatura i l'equació bàsica dels gasos MKT, podem escriure:
‹Ek›=3kT: 2
El valor mitjà de l'energia cinètica del moviment de les molècules de gas és proporcional a la seva temperatura. És a dir, la temperatura pot servir com a mesura de l'energia cinètica del moviment de les partícules.






