L'àlgebra proposicional és una ciència exacta que no compromet. Per resoldre exemples amb conjunció, disjunció, implicació, etc., podeu crear una taula de veritat a l'aplicació Excel. Està equipat amb un conjunt de funcions lògiques que automatitzen i faciliten el procés de cerca del resultat.
Lògica matemàtica: conceptes bàsics
Aristòtil és considerat el fundador de la lògica formal. Al segle XVII G. Leibniz va suggerir la introducció de símbols per definir enunciats. D. Buhl va consolidar els coneixements adquirits i per primera vegada va marcar frases amb símbols.
De manera esquemàtica, "VERTADER" se substitueix per 1 i "FALSE" per 0.
Sota l'enunciat s'entén tota frase declarativa que aporti qualsevol informació i sigui capaç de prendre el valor de veritat o falsedat. A l'àlgebra, les lògiques s'abstreuen de la càrrega semàntica de les frases i només tenen en compte els valors lògics.
La negació és una nova expressió que pren el valor de vertadera si és falsa i viceversa.
Conjunció de dosvariables s'anomena frase nova, que pren el valor de veritat en el cas de la designació simultània "1" i de falsedat en altres situacions.
La disjunció de dues afirmacions s'entén com una nova expressió que pren el valor "FALSE" només si hi ha "0" i "VERTADER" en altres variacions alhora.
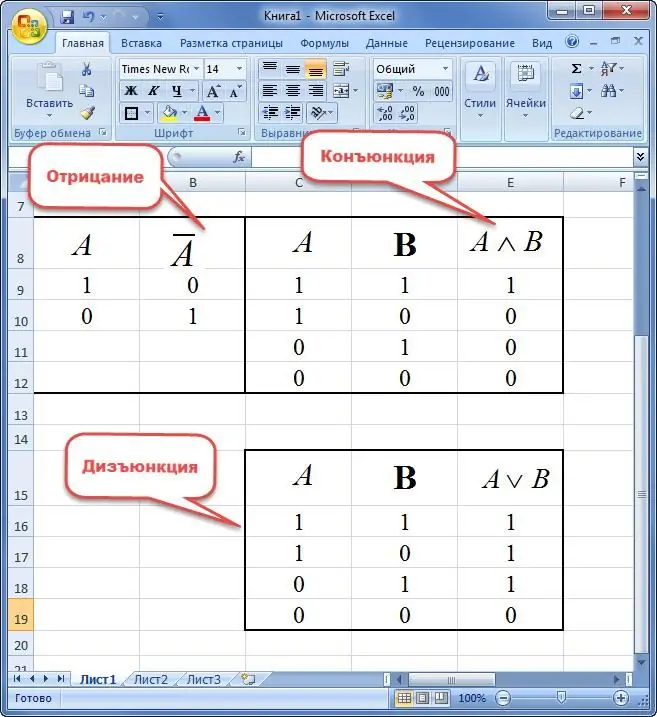
Una implicació de dues variables és una nova frase en la qual:
- si la premissa és certa i la conseqüència és falsa, aleshores l'expressió és igual a "0";
- sentència és igual a "1" en altres casos.
L'equivalent de dues variables s'entén com una nova afirmació que pren el valor de veritat només si els elements són els mateixos. En cas contrari, l'oferta és "0".
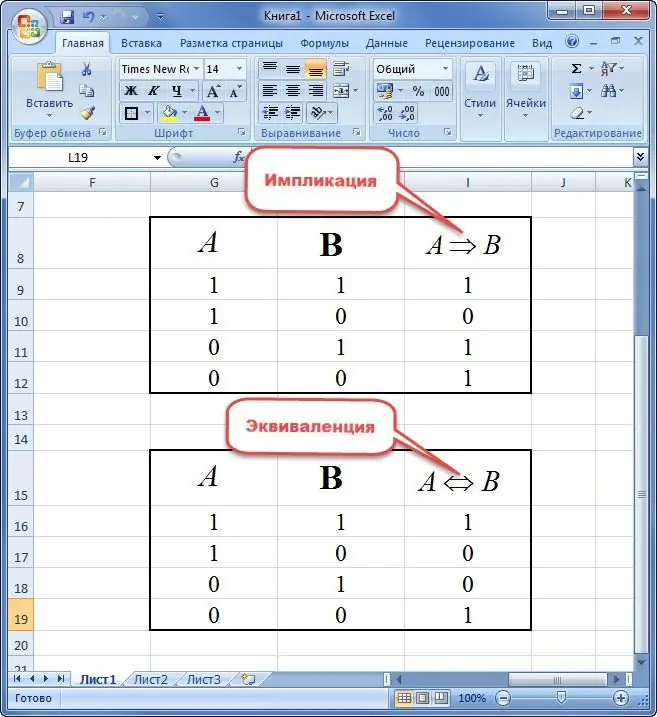
Els valors lògics de les expressions solen presentar-se en forma de taula. Hi ha un altre nom per a aquest tipus d'informació. Diuen que per a una declaració cal construir una taula de veritat. Especifica els valors inicials per a totes les variables i després es calcula el resultat de tota l'expressió.
Algorisme per implementar càlculs en operacions lògiques
Per construir una taula de veritat, cal saber l'ordre en què es realitzen les accions. En una expressió amb múltiples operands, el càlcul es realitza en l'ordre següent:
- inversió (negació);
- conjunció (funció lògica a Excel "I");
- disjunció (operador booleà a Excel "OR");
- implicació (conseqüència);
- equivalència.
Hi ha dues operacions més, però la seva prioritat no està definida:
- Ictus de Schaeffer;
- Perfora la fletxa.
L'algorisme de càlcul canvia si l'expressió està entre claudàtors.
L'ordre de construcció d'una forma tabular per a operands lògics a Excel
Abans de trobar el valor d'una expressió, cal estudiar el concepte de fórmula d'àlgebra lògica. La definició diu que aquesta és una expressió complexa, que consta de les declaracions més senzilles connectades per operands lògics.
Exemple 1. Construeix una taula de veritat per a la conjunció, la disjunció i la negació.
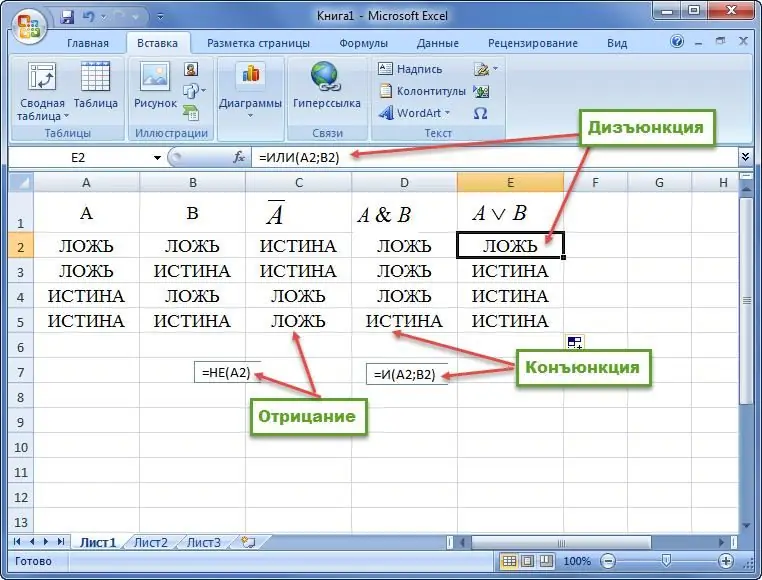
Exemple 2. Donada una fórmula per a l'àlgebra de la lògica. Construeix una taula de veritat. A continuació es donen exemples d'exemple.
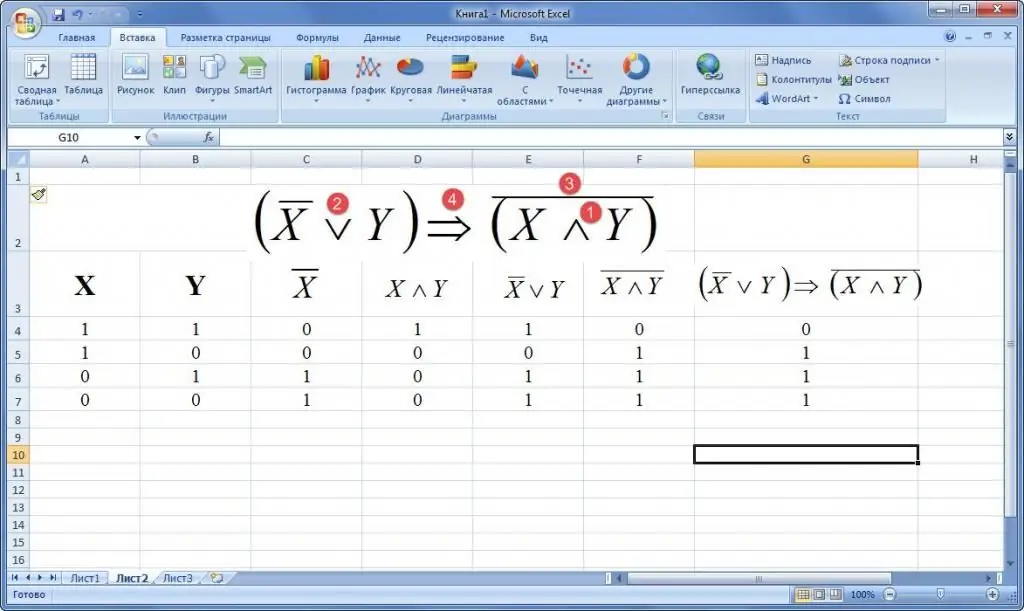
Exemple 3. Com construir una taula de veritat en Excel, donada una fórmula d'àlgebra lògica en una descripció verbal. Dient: "Si un triangle és equilàter, llavors totes les seves vores són iguals o tots els seus angles són iguals."
Primer, heu d'analitzar l'oració composta en elements mínims:
- La primera part de l'expressió: A="triangle equilàter".
- Segon: B="tots els costats de la figura són iguals".
- Tercer: C="tots els angles d'un triangle són iguals".
Després d'això, es compila i es resol una expressió al paquet de programari Excel.
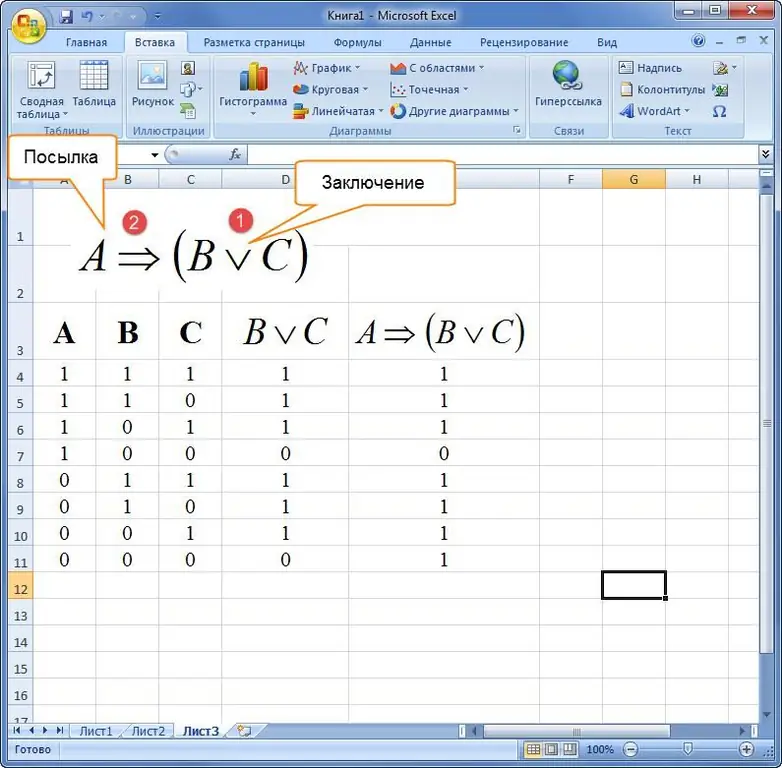
Quan compileu taules de veritat, és important recordar l'ordre de les operacions.






