La regla de Titius-Bode (de vegades anomenada simplement llei de Bode) és la hipòtesi que els cossos d'alguns sistemes orbitals, inclòs el Sol, giren al llarg dels semieixos en funció de la seqüència planetària. La fórmula suggereix que, estenent-se cap a l'exterior, cada planeta estarà aproximadament el doble de lluny del Sol que l'anterior.
La hipòtesi va predir correctament les òrbites de Ceres (al cinturó d'asteroides) i Urà, però no va poder determinar l'òrbita de Neptú i finalment va ser substituïda per la teoria de la formació del sistema solar. Porta el nom de Johann Daniel Titius i Johann Elert Bode.

Orígens
La primera menció d'una sèrie que s'aproxima a la llei de Bode es pot trobar a Elements of Astronomy de David Gregory, publicat el 1715. En ell diu: “… suposant que la distància del Sol a la Terra es divideix en deu parts iguals, de les quals la distància de Mercuri serà d'unes quatre, de Venus set, de Mart quinze, de Júpiter cinquanta-dos., i de Saturn noranta-cinc . Un suggeriment semblant, probablement inspirat en Gregory, apareix en una obra publicada per Christian Wolff el 1724.
L'any 1764, Charles Bonnet, al seu llibre Contemplation of Nature, va dir: "Coneixem els disset planetes que formen el nostre sistema solar [és a dir, els planetes principals i els seus satèl·lits], però no estem segurs que ja no hi són". A això, en la seva traducció de 1766 de l'obra de Bonnet, Johann Daniel Titius va afegir dos paràgrafs propis a la part inferior de la pàgina 7 i a la part superior de la pàgina 8. El nou paràgraf interpolat no es troba al text original de Bonnet: tampoc a l'italià. ni traduccions a l'anglès de l'obra.
Descobriment de Titius
Hi ha dues parts en el text intercalat de Titius. El primer explica la seqüència de distàncies planetàries respecte al Sol. També conté algunes paraules sobre la distància del Sol a Júpiter. Però aquest no és el final del text.
Val la pena dir unes quantes paraules sobre la fórmula de la regla de Titius-Bode. Fixeu-vos en les distàncies entre els planetes i descobriu que gairebé tots estan separats entre si en una proporció corresponent a la seva mida corporal. Dividiu la distància del Sol a Saturn per 100 parts; aleshores Mercuri està separat per quatre d'aquestes parts del Sol; Venus - en 4 + 3=7 d'aquestes parts; Terra - per 4+6=10; Mart - per 4+12=16.
Però tingueu en compte que de Mart a Júpiter hi ha una desviació d'aquesta progressió tan precisa. Un espai de 4+24=28 d'aquestes parts segueix de Mart, però fins ara no s'hi ha descobert ni un sol planeta. Però el Lord Arquitecte hauria de deixar aquest lloc buit? Mai. TanSuposem que aquest espai pertany sens dubte a les llunes encara no descobertes de Mart, i afegim que potser Júpiter encara té unes quantes llunes més petites al seu voltant que encara no han estat vistes per cap telescopi.

Rise of the Bode
El 1772, Johann Elert Bode, amb vint-i-cinc anys, va completar la segona edició del seu compendi astronòmic Anleitung zur Kenntniss des gestirnten Himmels ("Guia per al coneixement del cel estrellat"), al qual va va afegir la següent nota a peu de pàgina, originalment sense font, però anotada en versions posteriors. A les memòries de Bode es pot trobar una referència a Titius amb un clar reconeixement de la seva autoritat.

Opinió Bode
Així és com sona la regla de Titius-Bode en la presentació d'aquest últim: si la distància del Sol a Saturn es pren igual a 100, aleshores Mercuri està separat del Sol per quatre d'aquestes parts. Venus - 4+3=7. Terra - 4+6=10. Mart - 4+12=16.
Ara hi ha un buit en aquesta progressió ordenada. Després de Mart segueix un espai amb un càlcul de 4+24=28, en el qual encara no s'ha vist ni un sol planeta. Ens podem creure que el Fundador de l'univers va deixar aquest espai buit? És clar que no. A partir d'aquí arribem a la distància de Júpiter en forma de càlcul 4+48=52 i, finalment, a la distància de Saturn - 4+96=100.

Aquestes dues afirmacions sobre tota la tipologia específica i els radis orbitals semblen provenir de l'antiguitatastronomia. Moltes d'aquestes teories es remunten a abans del segle XVII.
Influència
Titius va ser alumne del filòsof alemany Christian Freiherr von Wolff (1679-1754). La segona part del text inserit a l'obra de Bonnet es basa en l'obra de von Wolff de 1723, Vernünftige Gedanken von den Wirkungen der Natur.
La literatura del segle XX assigna l'autoria de la regla Titius-Bode a un filòsof alemany. Si és així, Titius podria aprendre d'ell. Una altra referència més antiga va ser escrita per James Gregory el 1702 a la seva Astronomiae Physicae et geometryae Elementa, on la seqüència de distàncies planetàries 4, 7, 10, 16, 52 i 100 es va convertir en una progressió geomètrica de la proporció 2.
Aquesta és la fórmula més propera a Newton i també es va trobar als escrits de Benjamin Martin i Thomas Ceard anys abans que el llibre de Bonnet es publiqués a Alemanya.
Més treball i implicacions pràctiques
Titius i Bode esperaven que la llei conduís al descobriment de nous planetes i, de fet, el descobriment d'Urà i Ceres, la distància entre els quals concorda bé amb la llei, va contribuir a la seva acceptació pel món científic.
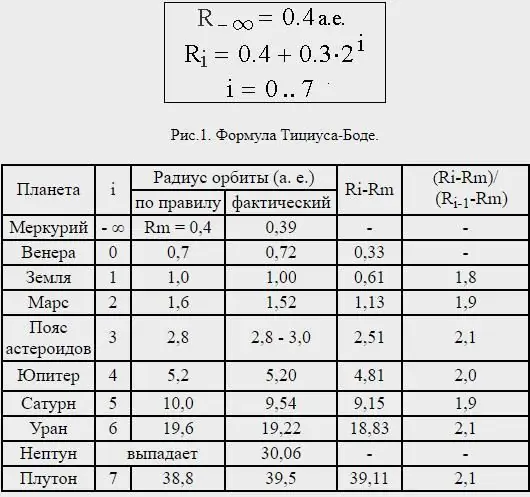
No obstant això, la distància de Neptú era molt inconsistent i, de fet, Plutó -ara no considerat un planeta- es troba a una distància mitjana que correspon aproximadament a la llei de Titius-Bode predita per al següent planeta fora d'Urà..
La llei publicada originalment va ser aproximadament satisfeta per tots els planetes coneguts, Mercuri i Saturn, amb una bretxa entrequart i cinquè planetes. Aquesta es va considerar una figura interessant, però no de gran importància fins al descobriment d'Urà el 1781, que encaixa en la sèrie.
Basant-se en aquest descobriment, Bode va demanar la recerca d'un cinquè planeta. Ceres, l'objecte més gran del cinturó d'asteroides, es va trobar a la posició prevista de Bode el 1801. La llei de Bode va ser àmpliament acceptada fins que Neptú va ser descobert el 1846 i es va demostrar que era incompatible amb la llei.
Al mateix temps, un gran nombre d'asteroides descoberts al cinturó van creuar Ceres fora de la llista de planetes. La llei de Bode va ser discutida per l'astrònom i lògic Charles Sanders Peirce l'any 1898 com a exemple de raonament enganyós.

Desenvolupament del problema
El descobriment de Plutó el 1930 va complicar encara més el problema. Tot i que no coincidia amb la posició predita per la llei de Bode, es tractava de la posició que la llei va predir per a Neptú. Tanmateix, el descobriment posterior del cinturó de Kuiper, i en particular de l'objecte Eris, que és més massiu que Plutó però no s'ajusta a la llei de Bode, va desacreditar encara més la fórmula.
Contribució de Serda
El jesuïta Thomas Cerda va impartir el famós curs d'astronomia a Barcelona l'any 1760 a la Càtedra Reial de Matemàtiques del Col·legi de Sant Jaume de Cordelle (Seminari Imperial i Reial dels Nobles de Cordell). Al Tratado de Cerdas apareixen les distàncies planetàries, obtingudes aplicant la tercera llei de Kepler, amb una precisió de 10-3.
Si prenem com a 10 la distància de la Terra iarrodoneix a un nombre enter, es pot expressar la progressió geomètrica [(Dn x 10) - 4] / [(Dn-1 x 10) - 4]=2, de n=2 a n=8. I utilitzant un moviment fictici uniforme circular a l'anomalia de Kepler, els valors de Rn corresponents a les proporcions de cada planeta es poden obtenir com rn=(Rn - R1) / (Rn-1 - R1), resultant en 1,82; 1, 84; 1, 86; 1,88 i 1,90, on rn=2 - 0,02 (12 - n) és una relació explícita entre la continuïtat kepleriana i la llei de Titius-Bode, que es considera una coincidència numèrica aleatòria. El resultat del càlcul s'aproxima a dos, però el dos es pot considerar com un arrodoniment del número 1, 82.

La velocitat mitjana del planeta des de n=1 fins a n=8 redueix la distància del Sol i difereix de la disminució uniforme a n=2 per recuperar-se de n=7 (ressonància orbital). Això afecta la distància del Sol a Júpiter. Tanmateix, la distància entre tots els altres objectes en el marc de la notòria regla a la qual es dedica l'article també està determinada per aquesta dinàmica matemàtica.
Aspecte teòric
No hi ha cap explicació teòrica sòlida subjacent a la regla de Titius-Bode, però és possible que donada la combinació de ressonància orbital i manca de graus de llibertat, qualsevol sistema planetari estable tingui una alta probabilitat de repetir el model descrit a aquesta teoria dels dos científics.
Com que pot ser una coincidència matemàtica i no una "llei de la naturalesa", de vegades s'anomena regla en lloc de "llei". Tanmateix, l'astrofísic Alan Boss argumenta que això és simplementcoincidència, i la revista de ciències planetàries Ícarus ja no accepta articles que intentin oferir versions millorades de la "llei".
Ressonància orbital
La ressonància orbital dels principals cossos en òrbita crea regions al voltant del Sol que no tenen òrbites estables a llarg termini. Els resultats de la simulació de formació de planetes donen suport a la idea que és probable que un sistema planetari estable escollit aleatòriament compleixi la regla de Titius-Bode.

Dubrulle i Graner
Dubrulle i Graner van demostrar que les regles de distància de la llei de poder poden ser una conseqüència de models de col·lapse de núvols de sistemes planetaris que tenen dues simetries: la invariància rotacional (el núvol i el seu contingut són axisimètrics) i la invariància d'escala (el núvol i el seu contingut). el seu contingut té el mateix aspecte a totes les escales).
Aquest últim és una característica de molts fenòmens que es creu que tenen un paper en la formació del planeta, com ara la turbulència. La distància del Sol als planetes del sistema solar, proposada per Titius i Bode, no va ser revisada en el marc dels estudis de Dubrulle i Graner.






