La termodinàmica de l'estat agregat gasós de la matèria és una branca important de la física que estudia l'equilibri termodinàmic i les transicions quasi estàtiques en sistemes. El model principal en què es basen les prediccions del comportament dels sistemes és el model de gas ideal. Amb el seu ús, es va obtenir l'equació de Mendeleiev-Clapeyron. Considereu-ho a l'article.
Gasolina ideal
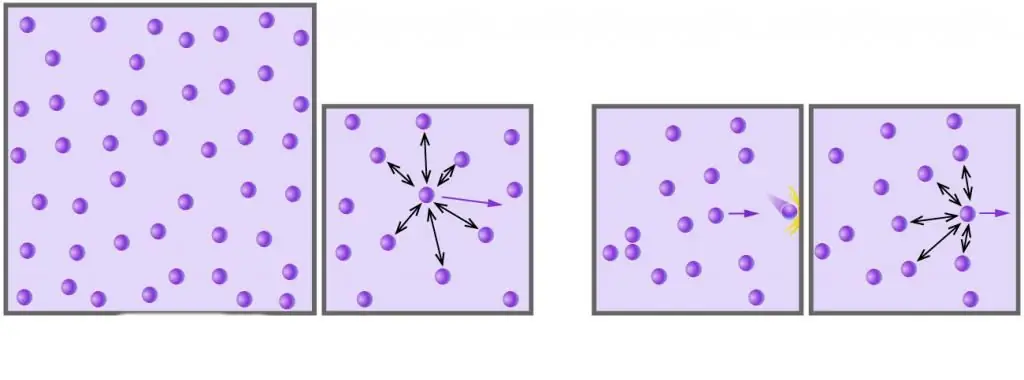
Com sabeu, tots els gasos reals estan formats per molècules o àtoms, les distàncies entre els quals són massa grans en comparació amb la seva mida a baixes pressions. A més, a altes temperatures, a escala absoluta, l'energia cinètica de les molècules supera la seva energia potencial associada a interaccions dipol-dipol febles (si, a més d'aquestes interaccions, hi ha altres tipus d'enllaços químics, per exemple, iònics o hidrogen, aleshores fan una contribució significativa al component potencial de l'energia del sistema intern).
A causa dePer a molts gasos reals en condicions properes a les normals, es poden descuidar les seves interaccions internes i la mida de les partícules. Aquestes dues aproximacions principals constitueixen el model de gas ideal.
L'equació de Mendeleev en física

És més correcte i just anomenar aquesta equació llei de Clapeyron-Mendeleev. El cas és que va ser enregistrat per primera vegada per l'enginyer francès Emile Clapeyron l'any 1834. Ho va fer analitzant les lleis dels gasos de Boyle-Mariotte, Gay-Lussac i Charles descobertes a principis del segle XIX.
El mèrit del químic rus Dmitry Mendeleiev rau en el fet que va donar a l'equació una forma matemàtica moderna i fàcil d'utilitzar. En particular, Mendeleiev va introduir a l'equació una constant per a tots els gasos R=8, 314 J/(molK). El mateix Clapeyron va utilitzar una sèrie de constants empíriques que dificulten el procés computacional.
L'equació de Mendeleiev-Clapeyron s'escriu de la següent manera:
PV=nRT.
Aquesta igu altat vol dir que el producte de la pressió P i el volum V al costat esquerre de l'expressió és sempre proporcional al producte de la temperatura absoluta T i la quantitat de substància n al costat esquerre.
L'expressió objecte d'estudi us permet obtenir qualsevol llei de gas si arregleu dos dels seus quatre paràmetres. En el cas dels isoprocessos s'estudien sistemes tancats en els quals no hi ha intercanvi de matèria amb el medi (n=const). Aquests processos es caracteritzen per un únic paràmetre termodinàmic fix (T, P o V).

Problema d'exemple
Ara resolem el problema de l'equació de Mendeleiev-Clapeyron. Se sap que l'oxigen que pesa 500 grams es troba en un cilindre amb un volum de 100 litres a una pressió de 2 atmosferes. Quina és la temperatura del globus, tenint en compte que el sistema està en equilibri termodinàmic.
Recordeu que, segons la definició, la quantitat d'una substància es calcula amb la fórmula:
n=m/M.
On m és la massa de totes les partícules del sistema, M és la seva massa molar mitjana. Aquesta igu altat ens permet reescriure l'equació de Mendeleiev de la forma següent:
PV=mRT/M.
On obtenim la fórmula de treball per a aquesta tasca:
T=PVM/(mR).
Queda per convertir totes les quantitats a unitats SI i substituir-les en aquesta expressió:
T=21013250, 10, 032/(0, 58, 314)=156 K.
La temperatura calculada és de -117 oC. Tot i que l'oxigen a aquesta temperatura encara és gasós (es condensa a -182,96 oC), en aquestes condicions el model de gas ideal només es pot utilitzar per obtenir una estimació qualitativa del valor calculat.






