Quan la revisió per parells, per exemple, s'avalua la competitivitat dels productes, és necessari, com en qualsevol treball científic, dur a terme un tractament de dades estadístiques. Aquest últim comença per determinar la coherència de les opinions d'experts, l'expressió numèrica de les quals és el coeficient de concordança.
Per què necessitem una avaluació de consens d'experts?
Aquesta avaluació és necessària, en primer lloc, perquè les opinions dels experts poden diferir molt sobre els paràmetres estimats. Inicialment, l'avaluació es realitza ordenant els indicadors i assignant-los un determinat coeficient de significació (pes). Una classificació inconsistent fa que aquests coeficients siguin estadísticament poc fiables. Les opinions dels experts amb el nombre requerit (més de 7-10) s'han de distribuir d'acord amb la llei normal.
El concepte del coeficient de concordança
Així. La coherència és concordança. El coeficient és una quantitat adimensional que mostra la relació entre la dispersió i la màxima dispersió en el cas general. Generalitzem aquests conceptes.
El coeficient de concordança és un nombre de 0 a 1, que mostra la coherència de les opinions dels experts quanclassificació d'algunes propietats. Com més a prop estigui aquest valor de 0, menor serà la consistència. Si el valor d'aquest coeficient és inferior a 0,3, les opinions dels experts es consideren inconsistents. Quan el valor del coeficient està en el rang de 0,3 a 0,7, la consistència es considera mitjana. Un valor superior a 0,7 es considera d' alta consistència.
Casos d'ús
Quan es realitza una investigació estadística, poden sorgir situacions en les quals un objecte es pot caracteritzar no per dues seqüències, que es processen estadísticament mitjançant el coeficient de concordança, sinó per diverses seqüències, que en conseqüència són classificades per experts amb el mateix nivell de professionalitat en una àrea determinada.
S'ha de determinar la coherència del rànquing realitzat pels experts per confirmar la veracitat de la hipòtesi que els experts fan mesures relativament precises, la qual cosa permet la formació de diverses agrupacions en grups d'experts, que estan determinats en gran part per factors humans, principalment, com ara diferències d'opinions, conceptes, diferents escoles científiques, la naturalesa de l'activitat professional, etc.
Breu descripció del mètode de classificació. Els seus avantatges i desavantatges
En classificar, s'utilitza el mètode de classificació. La seva essència rau en el fet que a cada propietat de l'objecte se li assigna un rang específic. A més, a cada expert inclòs en el grup d'experts se li assigna aquest rangde manera independent, la qual cosa comporta la necessitat de tractar aquestes dades per tal d'identificar la coherència de les opinions dels experts. Aquest procés es realitza calculant el coeficient de concordança.
El principal avantatge del mètode de classificació és la seva facilitat d'implementació.
Els principals desavantatges del mètode són:
- un nombre reduït d'objectes de classificació, ja que quan el seu nombre supera els 15-20, es fa difícil assignar puntuacions de classificació objectives;
- A partir de l'ús d'aquest mètode, la qüestió de fins a quin punt es troben els objectes estudiats entre si en significació roman oberta.
Quan s'utilitza aquest mètode, cal tenir en compte que les valoracions es basen en algun tipus de model probabilístic, per la qual cosa s'han d'aplicar amb precaució, donat l'abast.
Coeficient de rang de concordança de Kendall
S'utilitza per determinar la relació entre les característiques quantitatives i qualitatives que caracteritzen objectes homogenis i es classifiquen segons el mateix principi.
Aquest coeficient ve determinat per la fórmula:
t=2S/(n(n-1)), on
S: la suma de les diferències entre el nombre de seqüències i el nombre d'inversions a la segona funció;
n - nombre d'observacions.

Algorisme de càlcul:
- Els valors x es classifiquen en ordre ascendent o descendent.
- Els valors y s'ordenen en l'ordre en què corresponen als valors x.
- Per a cada rang successiu de y, determineu quants valors de rang superior el segueixen. Se sumen i es calcula la mesura de correspondència de seqüències de rangs en x i y.
- De la mateixa manera, es calcula el nombre de rangs de y amb valors més baixos, que també sumen.
- Afegiu el nombre de rangs amb valors més alts i el nombre de rangs amb valors més baixos, donant com a resultat el valor S.
Aquest coeficient mostra la relació entre dues variables i, en la majoria dels casos, s'anomena coeficient de correlació de rang Kendall. Aquesta dependència es pot representar gràficament.
Determinació del coeficient
Com es fa? Si el nombre de característiques o factors classificats supera 2, s'utilitza el coeficient de concordança, que, en essència, és una variant múltiple de la correlació de rang.
Ves amb compte. El càlcul del coeficient de concordança es basa en la proporció de la desviació de la suma de quadrats de rangs de la suma mitjana de quadrats de rangs, multiplicada per 12, al quadrat d'experts, multiplicada per la diferència entre el cub del nombre d'objectes i el nombre d'objectes.
Algorisme de càlcul
Per entendre d'on prové el nombre 12 al numerador de la fórmula de càlcul, mirem l'algoritme de determinació.
Per a cada línia amb els rangs d'un determinat expert, es calcula la suma dels rangs, que és un valor aleatori.
El coeficient de concordança es defineix generalment com la relació entre l'estimació de la variància (D) i el valor màxim de l'estimació de la variància(Dmàx). Anem a formular successivament les definicions d'aquestes magnituds.
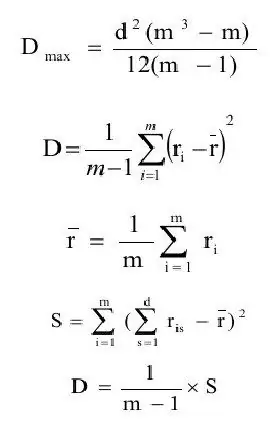
on rmitjana - estimació de les expectatives;
m - nombre d'objectes.
Substituint les fórmules resultants en relació a D per Dmax obtenim la fórmula final per al coeficient de concordança:
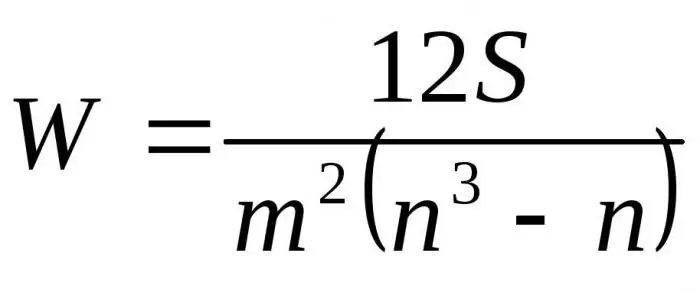
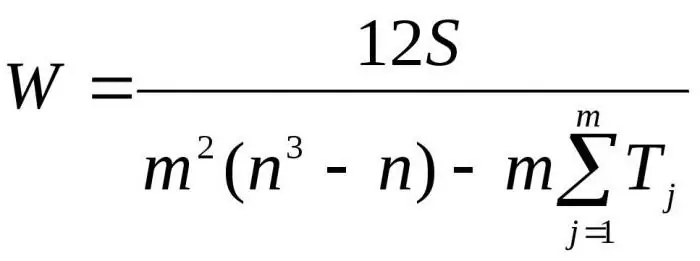
Aquí m és el nombre d'experts, n és el nombre d'objectes.
La primera fórmula s'utilitza per determinar el factor de concordança si no hi ha rangs relacionats. La segona fórmula s'utilitza si hi ha rangs relacionats.
Així que s'ha acabat el càlcul del coeficient de concordança. Que segueix? La significació del valor obtingut s'avalua mitjançant el coeficient de Pearson multiplicant aquest coeficient pel nombre d'experts i pel nombre de graus de llibertat (m-1). El criteri resultant es compara amb el valor de la taula, i si el valor del primer supera l'últim, parlen de la significació del coeficient objecte d'estudi.
En el cas de rangs relacionats, el càlcul del criteri de Pearson es fa una mica més complicat i es realitza amb la relació següent: (12S)/(d(m2+ m)-(1/(m-1))x(Ts1 +Ts2 +Tsn)
Exemple
Suposem que el mètode expert avalua la competitivitat de la mantega venuda en una xarxa minorista. Posem un exemple de càlcul del coeficient de concordança. Abans d'avaluar la competitivitat, cal classificar el consumidorpropietats d'aquest producte que participen en l'avaluació. Suposem que aquestes propietats seran les següents: gust i olor, consistència i aspecte, color, embalatge i etiquetatge, contingut de greix, nom comercial, fabricant, preu.
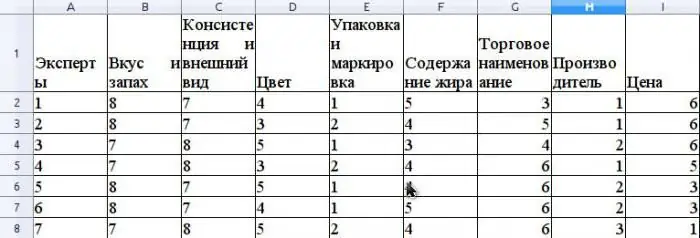
Suposem que el grup d'experts està format per 7 experts. La figura mostra els resultats de la classificació d'aquestes propietats.
El valor mitjà de r es calcula com a mitjana aritmètica i serà 31,5. Per trobar S, sumeu les diferències al quadrat entre ris i la mitjana de r, segons la fórmula anterior i determineu que el valor de S és 1718.
Calculeu el coeficient de concordança mitjançant la fórmula sense utilitzar rangs relacionats (els rangs estarien relacionats si el mateix assessor expert tingués els mateixos rangs per a diferents propietats).
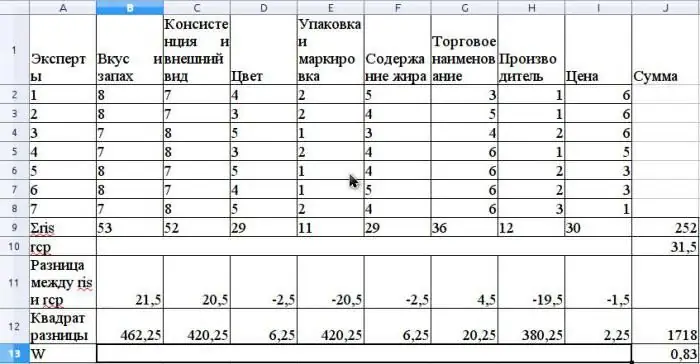
El valor d'aquest coeficient serà 0,83. Això indica un fort consens entre els experts.
Comproveu la seva importància mitjançant la prova de Pearson:
7 x 0,83 x (8-1)=40,7.
La prova tabular de Pearson amb un nivell de significació de l'1% és 18,5, i al 5% - 14,1..
L'exemple demostra la simplicitat i l'accessibilitat del càlcul per a qualsevol persona que conegui els fonaments bàsics dels càlculs matemàtics. Per pal·liar-los,utilitza formularis de full de càlcul.
En conclusió
Així, el coeficient de concordança mostra la coherència de les opinions de diversos experts. Com més lluny estigui de 0 i més a prop d'1, més coherents són les opinions. Aquests coeficients s'han de confirmar calculant el criteri de Pearson.






