Cada any augmenta l'interès per la programació. I si a les institucions especialitzades en programes d'escriptura es basen en un llenguatge de programació com C ++, a les escoles i escoles tècniques els estudiants es familiaritzen amb "Pascal". I ja a partir d'aquest llenguatge, comencen a comprendre la programació mitjançant l'ús del programari Delphi. Cal assenyalar de seguida que aquests llenguatges de programació ofereixen un espai enorme per a la manifestació de la seva imaginació. I si amb l'ajuda del llenguatge Pascal podeu familiaritzar-vos amb els conceptes bàsics de programació, a Delphi ja podeu escriure un programa complet. I de vegades un lloc força important en l'escriptura de programes l'ocupa la resolució de matrius en "Pascal".
La presència d'un gran nombre de variables molt diferents

Hi ha un munt de variables diverses en un llenguatge de programació, que es caracteritzen per la presència d'un sol valor. Són capaços d'emmagatzemar un sol valor que té un determinat tipus. Les variables de cadena són l'excepció. Ells sónés una col·lecció d'aquelles dades per a les quals és característic el tipus de caràcter. Però fins i tot aquestes variables solen considerar-se des de la posició d'un valor separat.
No és cap secret que amb l'ajuda d'un ordinador es pot reduir significativament el temps per realitzar determinades tasques relacionades amb grans quantitats de dades. Però, quan s'utilitzen només aquelles variables que tenen tipus coneguts pels humans, com és possible emmagatzemar els resultats del treball a la memòria i també processar aquelles dades que contenen un gran nombre de files? Aquestes tasques són força habituals en qualsevol camp d'activitat.
Per descomptat, sempre podeu introduir tantes variables com necessiteu per assolir els vostres objectius. També podeu definir alguns valors per a ells. Però el codi del programa només augmentarà a partir d'això. És difícil llegir el codi que té un gran nombre de línies. Sobretot quan cal trobar errors.
En conseqüència, els programadors van pensar en aquesta pregunta. És per això que els llenguatges que s'han desenvolupat fins ara tenen variables que permeten emmagatzemar en si mateixes una gran quantitat de dades. La matriu de "Pascal" ha canviat molt en l'enfocament de la programació. Per tant, es considera una variable important en un llenguatge de programació.
L'ús de matrius pot reduir dràsticament la mida del codi
Sota aquest terme s'amaga una seqüència ordenada de dades, que es caracteritza per un tipus. A més, totes aquestes dades reben el mateix nom. També hauriaCal tenir en compte que molts objectes del món real poden encaixar amb aquesta definició: diccionaris, dibuixos animats i molt més. Tanmateix, la manera més senzilla de presentar una matriu en "Pascal" és en forma d'una mena de taula. Cada cel·la individual conté una variable. Mitjançant les coordenades, podeu determinar la posició de la variable que ocuparà a la taula general.
Què vol dir una matriu unidimensional?
La taula més senzilla és la que és lineal. En aquesta matriu, per determinar la ubicació del paràmetre, n'hi ha prou amb especificar només un número. Es formen matrius més complexes a partir d'ells.
Per descriure matrius unidimensionals a "Pascal", només cal que introduïu el codi següent: escriviu Array of.
Els nombres són aquelles variables que poden tenir un tipus ordinal. Quan s'especifica un rang, val la pena entendre que el nombre inicial no pot ser superior al final. El tipus que tenen els elements de la matriu pot ser absolutament qualsevol cosa, ja sigui estàndard o ja descrit anteriorment. L'elecció dependrà de la necessitat de resoldre un problema concret.
Com es descriu una matriu lineal?
És possible descriure immediatament matrius unidimensionals en "Pascal". Això s'ha de fer en una secció especial, que és necessària per a aquest procediment en particular. Haureu d'introduir el codi següent: Var: Array Of.
Per entendre com podeu descriure una matriu en Pascal, heu d'introduir el codi següent:
- Var
- S, VV: Array[5..50] Of Real;
- K: Matriu[‘C’.. ‘R’] d’enter;
- Z: Matriu [-10..10] de Word;
- E: Matriu [3..30] Of Real.
En aquest exemple, les variables S, VV i T són una matriu d'aquests nombres que són reals. La variable K amaga el tipus de caràcter i aquests elements. Que són nombres enters. La matriu Z emmagatzema números el tipus dels quals és Word.
Entre totes les accions que es poden utilitzar quan es treballa amb una matriu, es pot distingir l'assignació. S'hi pot sotmetre tota la taula. Per exemple, S:=VV. Però cal entendre que les operacions d'assignació només es poden sotmetre a una matriu en "Pascal" que tingui un tipus determinat.
No hi ha més operacions que es puguin realitzar a tota la matriu alhora. Tanmateix, podeu treballar amb elements de la mateixa manera que amb altres nombres primers que tinguin un determinat tipus. Per fer referència a un paràmetre individual, heu d'especificar el nom de la matriu. Utilitzant claudàtors, heu de determinar l'índex que és característic de l'element desitjat. Per exemple: K[12].
Diferències principals entre matrius i altres variables
La diferència bàsica entre els components de la taula i les variables simples és que és possible posar entre parèntesis no només el valor de l'índex, sinó també una expressió que pot conduir al valor desitjat. Un exemple d'adreçament indirecte podria ser: V[K]. En aquest cas, la variable K pren un valor determinat. A partir d'aixòes dedueix que podeu utilitzar un bucle per omplir, processar i imprimir una matriu.
Aquesta forma d'organització es pot produir en el cas de variables de cadena prou properes en les seves propietats a matrius de tipus Char. Però també hi ha diferències. Són els següents:
- Les variables de cadena sempre es poden introduir des del teclat i imprimir-les a la pantalla.
- Les variables de cadena tenen una longitud limitada. Podeu introduir un màxim de 255 caràcters. La mida crítica de la matriu és de 64 kb.
Quins mètodes es poden utilitzar per mostrar dades de matriu a la pantalla?
Has de prestar atenció a la manera com es mostra el contingut de la matriu. N'hi ha diversos.
- Writeln (A[1], A[2], A[3]). Aquest exemple, encara que primitiu, és capaç de mostrar com es pot accedir directament a cada element individual inherent a la taula. Tanmateix, alguns dels avantatges que tenen les matrius de Pascal sobre les variables simples no són visibles aquí.
-
Programa A1;
Var B: matriu [1..10] d'enter;
K: enter;
Begin
Per a K:=1 a 10 Fes {Aquesta comanda fa un bucle amb el paràmetre }
Readln(A[K]); {A[I] s'està introduint amb el teclat }
For K:=10 Downto 1 Do {La taula s'imprimeix en ordre invers}
Write(A[K], 'VVV') Final.
Un codi similar del programa per a matrius en "Pascal" demostra com podeu introduir 10 números amb el teclat, imprimir-los, reordenant els valors en ordre invers. Si es reescriu el mateix programa des deutilitzant un gran nombre de variables en lloc d'una matriu, el codi augmentarà significativament. I això complica molt el procés de lectura del programa.
Augment de les possibilitats mitjançant l'ús de matrius

També és possible omplir taules amb valors que siguin iguals al quadrat dels índexs d'elements. També és possible crear aquesta matriu de cadenes en "Pascal", que permetrà introduir tots els números automàticament. Com podeu veure, l'ús d'una matriu millora molt les capacitats del llenguatge de programació Pascal.
El processament de matrius lineals és molt comú en diverses tasques. Per tant, no hi ha res estrany que s'estudiïn a instituts i escoles. A més, les possibilitats que ofereixen les matrius són força àmplies.
Què s'amaga sota les matrius bidimensionals?
Us podeu imaginar una taula que consta de diverses files alhora. Cada fila individual conté diverses cel·les. En aquesta situació, per determinar amb precisió la posició de les cel·les, cal marcar no un índex, com passava amb les matrius lineals, sinó dos números característics d'una fila i una columna. Les matrius bidimensionals a "Pascal" es caracteritzen per una representació similar.
Com descriure taules d'aquest tipus?
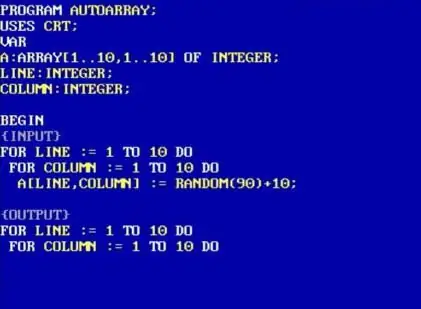
L'estructura de dades que es troba en el llenguatge Pascal per emmagatzemar els valors d'aquesta taula ésel nom d'una matriu bidimensional. La descripció d'aquesta matriu és possible immediatament mitjançant dos mètodes.
- Var B: matriu[1..15] de matriu [1..30] d'enter;
- Var B: matriu [1..15, 1..30] d'enter.
En tots aquests casos, es descriu una matriu bidimensional, que té 15 files i 30 columnes. Les descripcions que es van donar més amunt són absolutament equivalents. Per començar a treballar amb qualsevol dels elements, cal assignar dos índexs. Per exemple, A[6][5] o A[6, 5].
La sortida a la pantalla serà gairebé la mateixa que en el cas d'una matriu unidimensional. Només cal que especifiqueu dos índexs. En tots els altres aspectes, no hi ha diferències com a tals, de manera que no cal parlar-ne durant molt de temps.
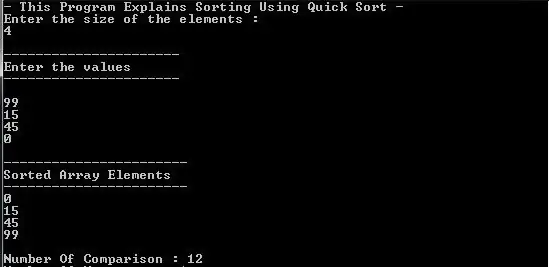
Primera manera d'ordenar
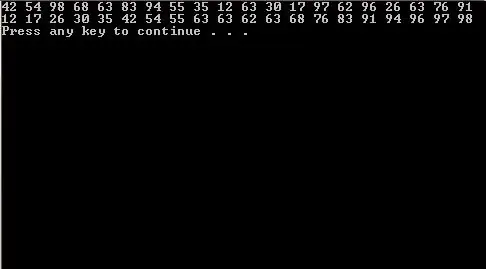
De vegades es fa necessari ordenar les dades. Per a això, el llenguatge té les ordres corresponents. Hi ha dos algorismes pels quals es pot ordenar una matriu en Pascal. El significat del mètode de selecció directa rau en el fet que en nidificar el bucle, absolutament totes les variables de la taula es compararan amb altres valors. En altres paraules, si hi ha una matriu de 15 números, el primer número 1 es compararà amb altres nombres. Això passarà fins que, per exemple, es trobi l'element que és més gran que el primer nombre. Posteriorment, la comparació tindrà lloc exactament aquesta xifra. Això es repetirà fins que es trobi el més gran.element de totes les propostes. Aquest mètode és bastant senzill per a aquells programadors que acaben de començar a treballar en l'idioma.
Mètode d'ordenació de la segona matriu
La segona manera és la bombolla. L'essència d'aquesta tècnica rau en el fet que els elements veïns es comparen per parelles. Per exemple, 1 i 2, 2 i 3, 3 i 4, etc. En cas que el valor trobat compleixi completament les condicions d'ordenació, es mourà al final de tota la matriu, és a dir, apareixerà com a "bombolla". Aquest algorisme és el més difícil de recordar. Tanmateix, no cal que el tritureu. El més important és entendre tota l'estructura del codi. I només en aquest cas es pot afirmar que s'aconsegueix grans alçades en la programació.
Conclusió

Esperem que entenguis què són les matrius i com pots ordenar per trobar un valor específic o assolir un objectiu concret. Si heu escollit "Pascal" per resoldre un problema en particular, en què les matrius ocupen un lloc important, haureu d'apropar-vos al seu estudi a fons. Això està influenciat per un factor com la presència en el llenguatge d'un nombre prou gran de variables que s'utilitzen en determinades situacions per simplificar tot el codi en conjunt. Les matrius es consideren correctament les quantitats principals, l'estudi de les quals s'ha de dur a terme sense fallar.






