Els patrons o patrons geomètrics naturals apareixen com a formes repetides que de vegades es poden descriure o representar mitjançant models matemàtics.
La geometria a la natura i la vida té moltes formes i formes, com ara simetria, espirals o ones.
Història
Per primera vegada, els filòsofs i científics grecs antics -Pitàgores, Empèdocles i Plató- van abordar qüestions de geometria a la natura. Mitjançant l'anàlisi d'exemples de formes geomètriques predictibles o ideals en plantes i animals, van intentar demostrar l'ordre i la simetria a la natura.
Els intents moderns d'estudiar la geometria a la natura van començar al segle XIX amb els esforços del físic belga Joseph Plateau, que va desenvolupar el concepte de la superfície mínima d'una bombolla de sabó. Els primers intents moderns es van concentrar primer a demostrar formes geomètriques ideals i predictibles, i després es van centrar en el desenvolupament de models que prediuen l'aparició i la manifestació de la geometria a la natura.
Al segle XX, el matemàtic Alan Turing va treballar en els mecanismes de la morfogènesi, que explica l'aparició en animalsdiversos patrons, ratlles, taques. Una mica més tard, el biòleg Aristide Lindenmeier, juntament amb el matemàtic Benoit Mandelbrot, completaran el treball sobre fractals matemàtics que repetien els patrons de creixement d'algunes plantes, inclosos els arbres.
Ciència
Les ciències modernes (matemàtiques, física i química), amb l'ajuda de tecnologies i models, intenten no només explicar, sinó també predir els patrons geomètrics que es troben a la natura.
La forma i el color de molts organismes vius, com ara el paó, els colibrís i les petxines marines, no només són bells, sinó que també són geomètricament correctes, la qual cosa atreu la curiositat dels científics. La bellesa que observem a la natura es pot produir de manera natural i matemàtica.
Els patrons naturals observats a les matemàtiques s'expliquen mitjançant la teoria del caos, que funciona amb espirals i fractals. Aquests patrons obeeixen les lleis de la física, a més, la física i la química, utilitzant matemàtiques abstractes, prediuen les formes dels cristalls, tant naturals com artificials.
La biologia explica la geometria de la natura mitjançant la selecció natural, on característiques tan regulars com ratlles, taques i colors brillants es poden explicar per la necessitat d'emmascarar o enviar senyals.
Tipus de patrons
A la natura, hi ha molts patrons repetits que apareixen en diverses formes geomètriques. Els tipus de regularitats bàsiques de la geometria a la natura, les fotos i les seves descripcions es poden trobar a continuació.
Simetria. Aquesta forma geomètrica és una de les més comunes a la natura. Més freqüent en animalssimetria del mirall: papallones, escarabats, tigres, mussols. També es troba en plantes, com ara fulles d'auró o flors d'orquídies. A més, la geometria simètrica a la natura pot ser radial, de cinc raigs o de sis vegades, com els flocs de neu.

Fractals. En matemàtiques, es tracta de construccions autosimilars que són infinites. A la natura, és impossible detectar una forma autorepetible tan infinita, per tant, les aproximacions de patrons fractals s'anomenen fractals geomètrics a la natura. Aquesta geometria es pot observar a la natura en fulles de falguera, bròquil, fruita de pinya.
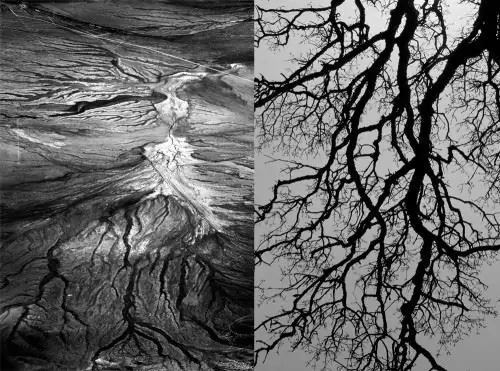
Espirals. Aquestes formes són especialment comunes entre els mol·luscs i els cargols. Els científics observen formes espirals a l'espai, per exemple, galàxies espirals. L'espiral s'anomena proporció àuria de Fibonacci.

Meandres. L'aleatorietat dels sistemes dinàmics en matemàtiques es manifesta a la natura en formes com meandres i fluxos. La geometria natural pren la forma d'una línia trencada o més aviat corba, com ara el cabal d'un riu.
Ones. Són causats per pertorbacions i moviments de l'aire, corrents de vent, propagats tant per l'aire com per l'aigua. A la natura, aquestes no només són ones del mar, sinó també dunes del desert, que poden formar formes geomètriques: línies, mitjanes i paràboles.
Mosaic. Creat repetint els mateixos elements a la superfície. La geometria del mosaic en la fauna es troba a les abelles: construeixenrusc de bresques - cèl·lules repetides.

Formació de patrons
En biologia, la formació d'un color geomètric es deu al procés de selecció natural. A mitjans del segle XX, Alan Turing va aconseguir descriure el mecanisme per a l'aparició de taques i ratlles en el color dels animals: el va anomenar model de reacció-difusió. Algunes cèl·lules del cos contenen gens que estan controlats per reaccions químiques. El morfògen condueix a la formació de zones de pell amb pigment fosc (taques i ratlles). Si el morfogen està present a totes les cèl·lules de la pell, s'obté el color de la pantera, si està present de manera desigual, el lleopard tacat habitual.






